Stokhos::Lanczos< vectorspace_type, operator_type > Class Template Reference

Applies Lanczos procedure to a given matrix. More...

#include <Stokhos_Lanczos.hpp>

Public Types
typedef operator_type::ordinal_type	ordinal_type
typedef operator_type::value_type	value_type
typedef Teuchos::SerialDenseVector < ordinal_type, value_type >	vector_type
typedef Teuchos::SerialDenseMatrix < ordinal_type, value_type >	matrix_type

Static Public Member Functions
static void	compute (ordinal_type k, const vectorspace_type &vs, const operator_type &A, const vector_type &u_init, matrix_type &u, Teuchos::Array< value_type > &alpha, Teuchos::Array< value_type > &beta, Teuchos::Array< value_type > &nrm_sqrd)
	Compute Lanczos basis.
static void	computeNormalized (ordinal_type k, const vectorspace_type &vs, const operator_type &A, const vector_type &u_init, matrix_type &u, Teuchos::Array< value_type > &alpha, Teuchos::Array< value_type > &beta, Teuchos::Array< value_type > &nrm_sqrd)
	Compute Lanczos basis.
static void	gramSchmidt (ordinal_type k, const vectorspace_type &vs, matrix_type &u, vector_type &u2)
	Gram-Schmidt orthogonalization routine.

Detailed Description

template<typename vectorspace_type, typename operator_type>
class Stokhos::Lanczos< vectorspace_type, operator_type >

Applies Lanczos procedure to a given matrix.

Given a matrix 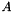, a starting vector 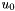, and integer 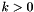, applies the Lanczos procedure to compute an orthogonal basis for the Krylov subspace

The basis vectors are given by

where $u_{-1} = 0$ and

Here 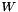is a diagonal weighting matrix.

---

The documentation for this class was generated from the following file:

• Stokhos_Lanczos.hpp