|
Stokhos
Development
|
|
Stokhos
Development
|


Public Member Functions | |
| Teuchos::RCP< const Teuchos::ParameterList > | getFastParameters () const |
| "Fast" but possibly unsafe or less accurate parameters. More... | |
Constructor/Destructor | |
| ICGSOrthoManager (const std::string &label="Belos", Teuchos::RCP< const OP > Op=Teuchos::null, const int max_ortho_steps=max_ortho_steps_default_, const MagnitudeType blk_tol=blk_tol_default_, const MagnitudeType sing_tol=sing_tol_default_) | |
| Constructor specifying re-orthogonalization tolerance. | |
| ICGSOrthoManager (const Teuchos::RCP< Teuchos::ParameterList > &plist, const std::string &label="Belos", Teuchos::RCP< const OP > Op=Teuchos::null) | |
| Constructor that takes a list of parameters. | |
| ~ICGSOrthoManager () | |
| Destructor. | |
Implementation of Teuchos::ParameterListAcceptorDefaultBase interface | |
| void | setParameterList (const Teuchos::RCP< Teuchos::ParameterList > &plist) |
|
Teuchos::RCP< const Teuchos::ParameterList > | getValidParameters () const |
Accessor routines | |
| void | setBlkTol (const MagnitudeType blk_tol) |
| Set parameter for block re-orthogonalization threshhold. | |
| void | setSingTol (const MagnitudeType sing_tol) |
| Set parameter for singular block detection. | |
| MagnitudeType | getBlkTol () const |
| Return parameter for block re-orthogonalization threshhold. | |
| MagnitudeType | getSingTol () const |
| Return parameter for singular block detection. | |
Error methods | |
|
Teuchos::ScalarTraits < ScalarType >::magnitudeType | orthonormError (const MV &X) const |
This method computes the error in orthonormality of a multivector, measured as the Frobenius norm of the difference innerProd(X,Y) - I. | |
|
Teuchos::ScalarTraits < ScalarType >::magnitudeType | orthonormError (const MV &X, Teuchos::RCP< const MV > MX) const |
This method computes the error in orthonormality of a multivector, measured as the Frobenius norm of the difference innerProd(X,Y) - I. The method has the option of exploiting a caller-provided MX. | |
|
Teuchos::ScalarTraits < ScalarType >::magnitudeType | orthogError (const MV &X1, const MV &X2) const |
This method computes the error in orthogonality of two multivectors, measured as the Frobenius norm of innerProd(X,Y). | |
|
Teuchos::ScalarTraits < ScalarType >::magnitudeType | orthogError (const MV &X1, Teuchos::RCP< const MV > MX1, const MV &X2) const |
This method computes the error in orthogonality of two multivectors, measured as the Frobenius norm of innerProd(X,Y). The method has the option of exploiting a caller-provided MX. | |
Label methods | |
| void | setLabel (const std::string &label) |
| This method sets the label used by the timers in the orthogonalization manager. | |
| const std::string & | getLabel () const |
| This method returns the label being used by the timers in the orthogonalization manager. | |
Static Public Attributes | |
Default orthogonalization constants | |
| static const int | max_ortho_steps_default_ |
| Max number of (re)orthogonalization steps, including the first (default). | |
| static const MagnitudeType | blk_tol_default_ |
| Block reorthogonalization threshold (default). | |
| static const MagnitudeType | sing_tol_default_ |
| Singular block detection threshold (default). | |
| static const int | max_ortho_steps_fast_ |
| Max number of (re)orthogonalization steps, including the first (fast). | |
| static const MagnitudeType | blk_tol_fast_ |
| Block reorthogonalization threshold (fast). | |
| static const MagnitudeType | sing_tol_fast_ |
| Singular block detection threshold (fast). | |
Orthogonalization methods | |
| void | project (MV &X, Teuchos::RCP< MV > MX, Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > > C, Teuchos::ArrayView< Teuchos::RCP< const MV > > Q) const |
Given a list of (mutually and internally) orthonormal bases Q, this method takes a multivector X and projects it onto the space orthogonal to the individual Q[i], optionally returning the coefficients of X for the individual Q[i]. All of this is done with respect to the inner product innerProd(). More... | |
| void | project (MV &X, Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > > C, Teuchos::ArrayView< Teuchos::RCP< const MV > > Q) const |
| This method calls project(X,Teuchos::null,C,Q); see documentation for that function. | |
| int | normalize (MV &X, Teuchos::RCP< MV > MX, Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > B) const |
This method takes a multivector X and attempts to compute an orthonormal basis for 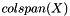 , with respect to innerProd(). More... , with respect to innerProd(). More... | |
| int | normalize (MV &X, Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > B) const |
| This method calls normalize(X,Teuchos::null,B); see documentation for that function. | |
| virtual int | projectAndNormalizeWithMxImpl (MV &X, Teuchos::RCP< MV > MX, Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > > C, Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > B, Teuchos::ArrayView< Teuchos::RCP< const MV > > Q) const |
Given a set of bases Q[i] and a multivector X, this method computes an orthonormal basis for ![$colspan(X) - \sum_i colspan(Q[i])$](form_151.png) . More... . More... | |
|
inline |
"Fast" but possibly unsafe or less accurate parameters.
Use this parameter list when you care more about speed than accuracy of the orthogonalization.
| int Belos::ICGSOrthoManager< Sacado::MP::Vector< Storage >, MV, OP >::normalize | ( | MV & | X, |
| Teuchos::RCP< MV > | MX, | ||
| Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > | B | ||
| ) | const |
This method takes a multivector X and attempts to compute an orthonormal basis for 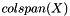 , with respect to innerProd().
, with respect to innerProd().
The method uses classical Gram-Schmidt, so that the coefficient matrix B is upper triangular.
This routine returns an integer rank stating the rank of the computed basis. If X does not have full rank and the normalize() routine does not attempt to augment the subspace, then rank may be smaller than the number of columns in X. In this case, only the first rank columns of output X and first rank rows of B will be valid.
The method attempts to find a basis with dimension the same as the number of columns in X. It does this by augmenting linearly dependant vectors in X with random directions. A finite number of these attempts will be made; therefore, it is possible that the dimension of the computed basis is less than the number of vectors in X.
| X | [in/out] The multivector to the modified. On output, X will have some number of orthonormal columns (with respect to innerProd()). |
| MX | [in/out] The image of X under the operator Op. If 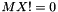 : On input, this is expected to be consistent with : On input, this is expected to be consistent with X. On output, this is updated consistent with updates to X. If 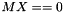 or or 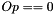 : : MX is not referenced. |
| B | [out] The coefficients of the original X with respect to the computed basis. The first rows in B corresponding to the valid columns in X will be upper triangular. |
| void Belos::ICGSOrthoManager< Sacado::MP::Vector< Storage >, MV, OP >::project | ( | MV & | X, |
| Teuchos::RCP< MV > | MX, | ||
| Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > > | C, | ||
| Teuchos::ArrayView< Teuchos::RCP< const MV > > | Q | ||
| ) | const |
Given a list of (mutually and internally) orthonormal bases Q, this method takes a multivector X and projects it onto the space orthogonal to the individual Q[i], optionally returning the coefficients of X for the individual Q[i]. All of this is done with respect to the inner product innerProd().
After calling this routine, X will be orthogonal to each of the Q[i]
The method uses either one or two steps of classical Gram-Schmidt. The algebraically equivalent projection matrix is 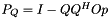 , if
, if Op is the matrix specified for use in the inner product. Note, this is not an orthogonal projector.
| X | [in/out] The multivector to be modified. On output, X will be orthogonal to Q[i] with respect to innerProd(). |
| MX | [in/out] The image of X under the operator Op. If 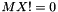 : On input, this is expected to be consistent with : On input, this is expected to be consistent with X. On output, this is updated consistent with updates to X. If 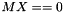 or or 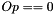 : : MX is not referenced. |
| C | [out] The coefficients of X in the *Q[i], with respect to innerProd(). If C[i] is a non-null pointer and *C[i] matches the dimensions of X and *Q[i], then the coefficients computed during the orthogonalization routine will be stored in the matrix *C[i]. If C[i] is a non-null pointer whose size does not match the dimensions of X and *Q[i], then a std::invalid_argument std::exception will be thrown. Otherwise, if C.size() < i or C[i] is a null pointer, then the orthogonalization manager will declare storage for the coefficients and the user will not have access to them. |
| Q | [in] A list of multivector bases specifying the subspaces to be orthogonalized against. Each Q[i] is assumed to have orthonormal columns, and the Q[i] are assumed to be mutually orthogonal. |
|
protectedvirtual |
Given a set of bases Q[i] and a multivector X, this method computes an orthonormal basis for ![$colspan(X) - \sum_i colspan(Q[i])$](form_151.png) .
.
This routine returns an integer rank stating the rank of the computed basis. If the subspace ![$colspan(X) - \sum_i colspan(Q[i])$](form_151.png) does not have dimension as large as the number of columns of
does not have dimension as large as the number of columns of X and the orthogonalization manager doe not attempt to augment the subspace, then rank may be smaller than the number of columns of X. In this case, only the first rank columns of output X and first rank rows of B will be valid.
The method attempts to find a basis with dimension the same as the number of columns in X. It does this by augmenting linearly dependant vectors with random directions. A finite number of these attempts will be made; therefore, it is possible that the dimension of the computed basis is less than the number of vectors in X.
| X | [in/out] The multivector to the modified. On output, the relevant rows of X will be orthogonal to the Q[i] and will have orthonormal columns (with respect to innerProd()). |
| MX | [in/out] The image of X under the operator Op. If 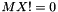 : On input, this is expected to be consistent with : On input, this is expected to be consistent with X. On output, this is updated consistent with updates to X. If 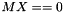 or or 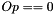 : : MX is not referenced. |
| C | [out] The coefficients of the original X in the Q[i], with respect to innerProd(). If C[i] is a non-null pointer and *C[i] matches the dimensions of X and *Q[i], then the coefficients computed during the orthogonalization routine will be stored in the matrix C[i]. If C[i] is a non-null pointer whose size does not match the dimensions of X and *Q[i], then *C[i] will first be resized to the correct size. This will destroy the original contents of the matrix. (This is a change from previous behavior, in which a std::invalid_argument exception was thrown if *C[i] was of the wrong size.) Otherwise, if C.size() < i<> or |
| B | [out] The coefficients of the original |
| Q | [in] A list of multivector bases specifying the subspaces to be orthogonalized against. Each |
Rank of the basis computed by this method.  1.8.5
1.8.5