Convergence test using the implicit residual norm(s), with an explicit residual norm(s) check for loss of accuracy if necessary. More...

#include <Belos_StatusTest_ImpResNorm_MP_Vector.hpp>

Detailed Description

Convergence test using the implicit residual norm(s), with an explicit residual norm(s) check for loss of accuracy if necessary.

This test passes when a quorum of residual vectors (for all right-hand sides) passes a residual norm test. For residual vector 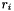$r_i$ , the form of the test is 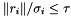$\|r_i\| / \sigma_i \le \tau$ , where 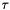$\tau$ is the convergence tolerance set in the constructor or by setTolerance(). The default quorum consists of all the vectors, but you can set the number of vectors that must pass before the whole test passes, either by the constructor argument or by calling setQuorum().

The default residual vector norm (the norm used in the numerator of the test, and applied to the current residual vectors) is the 2-norm, but you can change the norm type (1-norm, 2-norm, or infinity norm) using defineResForm(). The default scaling factor 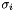$\sigma_i$ for residual vector i is the 2-norm of the initial residual vector, but you can change this using defineScaleForm(). The norm used for the scaling factors may be different than the norm used for the current residual vectors. 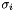Furthermore, each residual vector may use a different scaling factor $\sigma_i$ .

This test starts by using the "implicit" residual norm, otherwise called the "recursive" or "native" residual norm. It comes from the iterative method's projected problem, unlike the "explicit" residual norm, which comes from explicitly computing 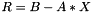$R = B - A * X$ . Once the implicit residual norm reaches the convergence tolerance, this test then checks the explicit residual norm to make sure that it has reached the convergence tolerance as well.

We say that there is a "potential loss of accuracy" when we first detect that the implicit residual norm(s) have met the desired original convergence tolerance, but the explicit residual norm(s) have not. We don't actually call this a "loss of accuracy" (in the sense of getLOADetected() returning true) unless we tried to remedy this situation, but couldn't fix it. Upon detecting a potential loss of accuracy, this test tells the solver to "iterate a few more steps" by making the "current" residual tolerance (the value of getCurrTolerance()) smaller, and forcing the implicit residual norm(s) to meet the current tolerance before moving on to test the explicit norm(s). If that doesn't work, this test declares a loss of accuracy.

This implementation is the same as the default, but is specialized for the Sacado::MP::Vector scalar type to keep track of when each component of the ensemble converges.

The documentation for this class was generated from the following file:

Belos_StatusTest_ImpResNorm_MP_Vector.hpp