More'-Thuente Line Search. Original code by Dianne O'Leary, modfified by Tammy Kolda and Roger Pawlowski for the NOX project. This version has been slightly optimized and also supports Homer Walker's work on adaptive forcing terms and Ared/Pred conditions. It also allows for arbitrary merit functions and norms to be supplied by the user. More...

#include <NOX_LineSearch_MoreThuente.H>

Inheritance diagram for NOX::LineSearch::MoreThuente:

[legend]

Collaboration diagram for NOX::LineSearch::MoreThuente:

[legend]

Public Member Functions
	MoreThuente (const Teuchos::RCP< NOX::GlobalData > &gd, Teuchos::ParameterList &params)
	Constructor.

	~MoreThuente ()
	Destructor.

bool	reset (const Teuchos::RCP< NOX::GlobalData > &gd, Teuchos::ParameterList &params)

bool	compute (NOX::Abstract::Group &newgrp, double &step, const NOX::Abstract::Vector &dir, const NOX::Solver::Generic &s)
	Perform a line search. More...

Public Member Functions inherited from NOX::LineSearch::Generic
	Generic ()
	Default constructor.

virtual	~Generic ()
	Destructor.

Detailed Description

More'-Thuente Line Search. Original code by Dianne O'Leary, modfified by Tammy Kolda and Roger Pawlowski for the NOX project. This version has been slightly optimized and also supports Homer Walker's work on adaptive forcing terms and Ared/Pred conditions. It also allows for arbitrary merit functions and norms to be supplied by the user.

This code is based on the More'-Thuente line search from the 1983 MINPACK Project. More specifically, this code is based on Dianne O'Leary's 1991 Matlab-implementation of the More'-Thuente line search. The original comments are preserved in the descriptions of the individual subroutines. What follows is an updated summary.

The merit function we are minimizing is given by

$f(x) = 0.5 \|F(x)\|^2$

(alternatively the user can define this)

The purpose of the More'-Thuente line search is to find a step which satisfies a sufficient decrease condition and a curvature condition. At each stage the subroutine updates an interval of uncertainty with endpoints stx and sty. The interval of uncertainty is initially chosen so that it contains a minimizer of the modified function

$f(x+{\rm stp} \; s) - f(x) - {\rm ftol} \; {\rm stp} \; (\nabla f(x)^T s).$

If a step is obtained for which the modified function has a nonpositive function value and nonnegative derivative, then the interval of uncertainty is chosen so that it contains a minimizer of 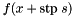$f(x+{\rm stp}\;s)$ .

The algorithm is designed to find a step which satisfies one of two sufficient decrease conditions:

(1) Armijo-Goldstein Condition

$f(x + {\rm stp} \; s) \le f(x) + {\rm ftol} \; {\rm stp} \; (\nabla f(x)^T s),$

or

(2) Ared/Pred Condtition

$F(x_{n-1}+ \lambda s) \le F(x_{n-1})(1-\alpha(1-\eta))$

and the curvature condition

$\vert \nabla f(x + {\rm stp} \; s)^T s) \vert \le {\rm gtol} \; |\nabla f(x)^T s|$

If ftol is less than gtol and if, for example, the function is bounded below, then there is always a step which satisfies both conditions. If no step can be found which satisfies both conditions, then the algorithm usually stops when rounding errors prevent further progress. In this case stp only satisfies the sufficient decrease condition.

Modifications from NOX::LineSearch::MoreThuente

Added the option to use Ared/Pred conditions as describe in Homer Walker's papers.
Added support to use an adjustable forcing term as describe in Homer Walker's papers.
Added the option to use directional derivatives in computing the slope instead of explicitly computing the Jacobian. This eliminates the need to recompute the Jacobian at each inner iteration of the More'-Thuente algorithm.
Added the ability to use the NOX::Parameter::UserNorm and NOX::Parameter::MeritFunction objects to supply user defined norms and merit functions to the line search.

Implementation
This line search can be called via NOX::LineSearch::Manager.

This line search is used if "More'-Thuente" is the "Method" in the "Line Search" sublist. (See NOX::LineSearch::Manager for details.)

The following parameters can be specified for this line search in the "More'-Thuente" sublist of the "Line Search" sublist:

"Sufficient Decrease Condition" - Choice to use for the sufficient decrease condition. Options are "Ared/Pred" or "Armijo-Goldstein" (defaults to "Armijo-Goldstein").

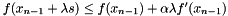
"Armijo-Goldstein" conditions: $f(x_{n-1}+ \lambda s) \le f(x_{n-1}) +\alpha \lambda f'(x_{n-1})$
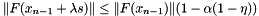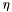"Ared/Pred" conditions: $\| F(x_{n-1}+ \lambda s) \| \le \| F(x_{n-1}) \| (1-\alpha(1-\eta))$ where $\eta$ is the linear solve tolerance in the inexact Newton method.

"Sufficient Decrease" - The ftol in the sufficient decrease condition (defaults to 1.0e-4)
"Curvature Condition" - The gtol in the curvature condition (defaults to 0.9999)
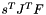"Optimize Slope Calculation" - Boolean value. If set to true the value of is estimated using a directional derivative in a call to NOX::LineSearch::Common::computeSlopeWithOutJac. If false the slope computation is computed with the NOX::LineSearch::Common::computeSlope method. Setting this to true eliminates having to compute the Jacobian at each inner iteration of the More'-Thuente line search (defaults to false).
"User Defined Norm" - The user can redefine the norm that is used in the Ared/Pred sufficient decrease condition by supplying a NOX::Parameter::UserNorm derived object in the parameter list with this key.
"Merit Function" - The user can supply their own merit function to the line search by supplying a NOX::Parameter::MeritFunction derived object with this key.
"Interval Width" - The maximum width of the interval containing the minimum of the modified function (defaults to 1.0e-15)
"Maximum Step" - maximum allowable step length (defaults to 1.0e6)
"Minimum Step" - minimum allowable step length (defaults to 1.0e-12)
"Max Iters" - maximum number of right-hand-side and corresponding Jacobian evaluations (defaults to 20)
"Default Step" - starting step length (defaults to 1.0)
"Recovery Step Type" - Determines the step size to take when the line search fails. Choices are:
- "Constant" [default] - Uses a constant value set in "Recovery Step".
- "Last Computed Step" - Uses the last value computed by the line search algorithm.
"Recovery Step" - The value of the step to take when the line search fails. Only used if the "Recovery Step Type" is set to "Constant". Defaults to value for "Default Step".

Output Parameters
A sublist for output parameters will be created called "Output" in the parameter list used to instantiate or reset the class. Valid output parameters are:

"Total Number of Line Search Calls" - Total number of calls to the compute() method of this line search.
"Total Number of Non-trivial Line Searches" - The total number of steps that could not directly take a full step and meet the required "Convergence Criteria" (i.e. The line search had to reduce the step length using inner iteration calculations over iterate ).
"Total Number of Failed Line Searches" - total number of line searches that failed and used a recovery step.
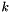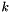"Total Number of Line Search Inner Iterations" - total number of inner iterations performed by this object.

Member Function Documentation

bool NOX::LineSearch::MoreThuente::compute	(	NOX::Abstract::Group &	grp,
		double &	step,
		const NOX::Abstract::Vector &	dir,
		const NOX::Solver::Generic &	s
	)

virtual

Perform a line search.

On input:

Parameters

grp	The initial solution vector, 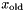$x_{\rm old}$ .
dir	A vector of directions to be used in the line search, .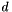
s	The nonlinear solver.

On output:

Parameters

step	The distance the direction was scaled, 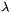$\lambda$ .
grp	The `grp` is updated with a new solution, 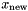$x_{\rm new}$ , resulting from the linesearch. Normally, for a single direction line search, this is computed as:

$x_{\rm new} = x_{\rm old} + \lambda d.$

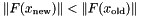Ideally, $\|F(x_{\rm new})\| < \|F(x_{\rm old})\|$ (e.g the final direction is a descent direction).

Note that the dir object is a std::vector. For typical line searches as described in the above equation, this vector is of size one. We have used a std::vector to allow for special cases of multi-directional line searches such as the Bader/Schnabel curvillinear line search.

Return value is true for a successful line search computation.

Implements NOX::LineSearch::Generic.

References NOX::Solver::Generic::getPreviousSolutionGroup().

The documentation for this class was generated from the following files:

NOX_LineSearch_MoreThuente.H
NOX_LineSearch_MoreThuente.C

Public Member Functions

Detailed Description

Member Function Documentation