|
ConstrainedOptPack: C++ Tools for Constrained (and Unconstrained) Optimization
Version of the Day
|
|
ConstrainedOptPack: C++ Tools for Constrained (and Unconstrained) Optimization
Version of the Day
|
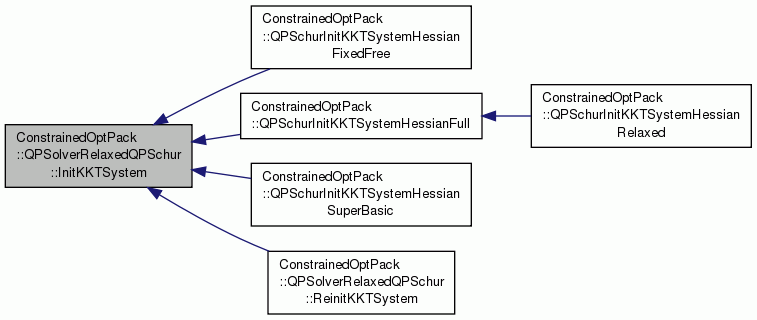
Interface for the object that forms the initial KKT system {abstract}. More...
#include <ConstrainedOptPack_QPSolverRelaxedQPSchur.hpp>
Public Types | |
| typedef std::vector< size_type > | i_x_free_t |
| typedef std::vector< size_type > | i_x_fixed_t |
| typedef std::vector< EBounds > | bnd_fixed_t |
| typedef std::vector< size_type > | j_f_decomp_t |
| typedef Teuchos::RCP< const MatrixSymOpNonsing > | Ko_ptr_t |
Public Member Functions | |
| virtual | ~InitKKTSystem () |
| virtual void | initialize_kkt_system (const Vector &g, const MatrixOp &G, value_type etaL, const Vector *dL, const Vector *dU, const MatrixOp *F, BLAS_Cpp::Transp trans_F, const Vector *f, const Vector *d, const Vector *nu, size_type *n_R, i_x_free_t *i_x_free, i_x_fixed_t *i_x_fixed, bnd_fixed_t *bnd_fixed, j_f_decomp_t *j_f_decomp, DVector *b_X, Ko_ptr_t *Ko, DVector *fo) const =0 |
| Initializes the KKT system. More... | |
Interface for the object that forms the initial KKT system {abstract}.
Note that this interface is set up such that the relaxation variable must always be initially fixed (and rightly so to avoid illconditioning).
Definition at line 71 of file ConstrainedOptPack_QPSolverRelaxedQPSchur.hpp.
| typedef std::vector<size_type> ConstrainedOptPack::QPSolverRelaxedQPSchur::InitKKTSystem::i_x_free_t |
Definition at line 74 of file ConstrainedOptPack_QPSolverRelaxedQPSchur.hpp.
| typedef std::vector<size_type> ConstrainedOptPack::QPSolverRelaxedQPSchur::InitKKTSystem::i_x_fixed_t |
Definition at line 76 of file ConstrainedOptPack_QPSolverRelaxedQPSchur.hpp.
| typedef std::vector<EBounds> ConstrainedOptPack::QPSolverRelaxedQPSchur::InitKKTSystem::bnd_fixed_t |
Definition at line 78 of file ConstrainedOptPack_QPSolverRelaxedQPSchur.hpp.
| typedef std::vector<size_type> ConstrainedOptPack::QPSolverRelaxedQPSchur::InitKKTSystem::j_f_decomp_t |
Definition at line 80 of file ConstrainedOptPack_QPSolverRelaxedQPSchur.hpp.
| typedef Teuchos::RCP<const MatrixSymOpNonsing> ConstrainedOptPack::QPSolverRelaxedQPSchur::InitKKTSystem::Ko_ptr_t |
Definition at line 83 of file ConstrainedOptPack_QPSolverRelaxedQPSchur.hpp.
|
inlinevirtual |
Definition at line 85 of file ConstrainedOptPack_QPSolverRelaxedQPSchur.hpp.
|
pure virtual |
Initializes the KKT system.
Let the following permutation matrices define the selection of the initial KKT system:
Q = [ Q_R, Q_X ] : Initially fixed Q_R and free Q_X variables
P = [ P_d, P_u ] : Decomposed P_d and undecomposed P_u constraints
Given the definitions of Q and P above, this function will return the initial KKT system:
Ko = [ Q_R'*G*Q_R Q_R'*op(F')*P_d ]
[ P_d'*op(F)*Q_R 0 ]
fo = [ -Q_R'*g - Q_R'*G*Q_X*b_X ]
[ -P_d'f - P_d'*op(F)*Q_X*b_X ]
b_X = ??? (see below)
| g | [in] See QPSolverRelaxed::solve_qp() |
| G | [in] See QPSolverRelaxed::solve_qp() |
| dL | [in] See QPSolverRelaxed::solve_qp() |
| dU | [in] See QPSolverRelaxed::solve_qp() |
| F | [in] See QPSolverRelaxed::solve_qp() |
| trans_f | [in] See QPSolverRelaxed::solve_qp() |
| f | [in] See QPSolverRelaxed::solve_qp() |
| d | [in] See QPSolverRelaxed::solve_qp() |
| nu | [in] See QPSolverRelaxed::solve_qp() |
| n_R | [out] Number of initially free variables. |
| i_x_free | [out] array (size n_R or 0): If i_x_free.size() > 0 then i_x_free[l-1], l = 1...n_R defines the matrix Q_R as:Q_R(:,l) = e(i_x_free[l-1]), l = 1...n_RIf i_x_free.size() == 0 then i_x_free is implicitly identity and Q_R is defiend as:Q_R(:,l) = e(l), l = 1...n_RThe ordering of these indices is significant. |
| i_x_fixed | [out] array (size n_X): i_x_fixed[l-1], l = 1...n_X defines the matrix Q_X as:Q_X(:,l) = e(i_x_fixed[l-1]), l = 1...n_XThe ordering of these indices is significant. |
| bnd_fixed | [out] array (size n_X): bnd_fixed[l-1], l = 1...n_X defines the initial active set as: / LOWER : b_X(l) = dL(i_x_fixed[l-1])
bnd_fixed[l-1] = | UPPER : b_X(l) = dU(i_x_fixed[l-1])
\ EQUALITY : b_X(l) = dL(i) = dU(i) (i = i_x_fixed[l-1])
|
| j_f_decomp | [out] array (size m): j_f_decomp[p-1], p = 1...m defines the decomposed equalities included in Ko as:P_d(:,p) = e(j_f_decomp[p-1]), p = 1...mThe ordering of these indices is significant and are not necessarily sorted in assending or decending order. |
| b_X | [out] vector (size n_X): Initial varaible bounds (see bnd_fixed above). Note that the relaxation variable is always one of the initially fixed variables. |
| Ko | [in/out] Initial KKT matrix (size (n_R+m) x (n_R+m)). On output, Ko will contain a possibly dynamically allocated nonsingular matrix object that represents Ko. In input, if Ko->get() != NULL, and no other objects have a reference to this object (based on Ko->count(), and it is of the proper type, then this matrix may be reused. |
| fo | [out] vector (size n_R + m) of the rhs for the initial KKT system. |
Implemented in ConstrainedOptPack::QPSchurInitKKTSystemHessianFull.
 1.8.6
1.8.6