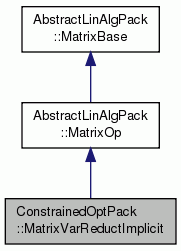
Implements D = - inv(C) * N for a variable reduction projection. More...

#include <ConstrainedOptPack_MatrixVarReductImplicit.hpp>

Inheritance diagram for ConstrainedOptPack::MatrixVarReductImplicit:

Public types
typedef Teuchos::RCP< const MatrixOpNonsing >	mat_nonsing_ptr_t

typedef Teuchos::RCP< const MatrixOp >	mat_ptr_t

Constructors / initializers
virtual void	initialize (const mat_nonsing_ptr_t &C, const mat_ptr_t &N, const mat_ptr_t &D_direct)
	Initialize `this` matrix object. More...

virtual void	set_uninitialized ()
	Set the matrix to uninitialized. More...

Access
const mat_nonsing_ptr_t &	C_ptr () const
	Return the smart pointer to the aggregate basis matrix object `C`. More...

const mat_ptr_t &	N_ptr () const
	Return the smart pointer to the aggregate nonbasis matrix object `N`. More...

const mat_ptr_t &	D_direct_ptr () const
	Return the smart pointer to the aggregate precomputed matrix object `D_direct` (if set). More...

Overridden from MatrixBase.
size_type	rows () const

size_type	cols () const

Overridden from MatrixOp.
const VectorSpace &	space_cols () const

const VectorSpace &	space_rows () const

MatrixOp &	operator= (const MatrixOp &M)

std::ostream &	output (std::ostream &) const

void	Vp_StMtV (VectorMutable *v_lhs, value_type alpha, BLAS_Cpp::Transp trans_rhs1, const Vector &v_rhs2, value_type beta) const

void	Vp_StMtV (VectorMutable *v_lhs, value_type alpha, BLAS_Cpp::Transp trans_rhs1, const SpVectorSlice &sv_rhs2, value_type beta) const

void	Vp_StPtMtV (VectorMutable *v_lhs, value_type alpha, const GenPermMatrixSlice &P_rhs1, BLAS_Cpp::Transp P_rhs1_trans, BLAS_Cpp::Transp M_rhs2_trans, const Vector &v_rhs3, value_type beta) const

void	Vp_StPtMtV (VectorMutable *v_lhs, value_type alpha, const GenPermMatrixSlice &P_rhs1, BLAS_Cpp::Transp P_rhs1_trans, BLAS_Cpp::Transp M_rhs2_trans, const SpVectorSlice &sv_rhs3, value_type beta) const

Detailed Description

Implements D = - inv(C) * N for a variable reduction projection.

This class is used to implement an implicit matrix defined as

D = - inv(C) * N

The operations y = op(D)*x are implemented as:

 y = D * x
   = -inv(C) * (N * x)

 y = D' * x
   = - N' * (inv(C') * x)

This class also allows the client to set a precomputed matrix D_direct that represents D = -inv(C)*N that will be used to extract rows or columns or to implement operations involving GenPermMatrixSlice when convenient. One might ask why this subclass would even be used if D_direct was even available. The reason is that it may be cheaper to perform the sparse solve and matrix-vector multiplication with C and N than it is to use a dense precomputed matrix D_direct. Determining if this class is even useful when D_direct is availible must be determined at runtime using timing data (which can be very hard to do well in general).

This implementation is designed to deal efficiently with the case where matrix- vector multiplications will only be performed with subsets of rows of inv(C)*N or columns of N'inv(C'). This primarily affects two types of operations:




y = b*y + a[-N'inv(C')]*x (x is a SpVectorSlice object) 

 y = b*y + a*op(P)[-inv(C)*N]*x (P has few nonzeros, x is any vector)

when D_direct is not set then needed rows of inv(C)*N are generated on the fly (as abstract vectors) and stored away for later use. When this->initialize() is called then all of these computed rows are discarded and they must be generated again.

Definition at line 91 of file ConstrainedOptPack_MatrixVarReductImplicit.hpp.

Member Typedef Documentation

typedef Teuchos::RCP<const MatrixOpNonsing> ConstrainedOptPack::MatrixVarReductImplicit::mat_nonsing_ptr_t

Definition at line 100 of file ConstrainedOptPack_MatrixVarReductImplicit.hpp.

typedef Teuchos::RCP<const MatrixOp> ConstrainedOptPack::MatrixVarReductImplicit::mat_ptr_t

Definition at line 102 of file ConstrainedOptPack_MatrixVarReductImplicit.hpp.

Member Function Documentation

void ConstrainedOptPack::MatrixVarReductImplicit::initialize	(	const mat_nonsing_ptr_t &	C,
		const mat_ptr_t &	N,
		const mat_ptr_t &	D_direct
	)

virtual

Initialize this matrix object.

Parameters

C	[in] Nonsingular basis matrix object. This matrix object must not be altered while `this` is in use or until `this->initialize()` is called again.
N	[in] Genaral nonbasis matrix object. This matrix object must not be altered while `this` is in use or until `this->initialize()` is called again.
D_direct	[in] Matrix object for `D = -inv(C)*N` already computed. The matrix object `D_direct` will not be modifed by `this` and must not be altered while c\ this matrix object is in use or until `this->initialize()` is called again. `D_direct == NULL` is allowed and `this` matrix object will just have to do without. For most applications (except those using direct linear solvers for `C` and when `N` has many columns) `D_direct` should be set to `NULL` and should not be computed by the client (that is the whole purpose for this matrix class).

Preconditions:

C.get() != NULL (throw std::invalid_argument)
N.get() != NULL (throw std::invalid_argument)
[D_direct != NULL] D_direct->space_cols().is_compatible(C->space_cols()) == true && D_direct->space_rows().is_compatible(N->space_rows()) == true (throw VectorSpace::IncompatibleVectorSpaces)

Postconditions:

this->C_ptr().get() == C.get()
this->N_ptr().get() == N.get()
this->D_direct_ptr().get() == N.get()

Definition at line 197 of file ConstrainedOptPack_MatrixVarReductImplicit.cpp.

void ConstrainedOptPack::MatrixVarReductImplicit::set_uninitialized ( )

virtual

Set the matrix to uninitialized.

Postconditions:

this->C_ptr().get() == NULL
this->N_ptr().get() == NULL
this->D_direct_ptr().get() == NULL

Definition at line 239 of file ConstrainedOptPack_MatrixVarReductImplicit.cpp.

const MatrixVarReductImplicit::mat_nonsing_ptr_t & ConstrainedOptPack::MatrixVarReductImplicit::C_ptr ( ) const

inline

Return the smart pointer to the aggregate basis matrix object C.

If this is the only reference to this matrix object, then return.count() == 1 will be true.

Definition at line 284 of file ConstrainedOptPack_MatrixVarReductImplicit.hpp.

const MatrixVarReductImplicit::mat_ptr_t & ConstrainedOptPack::MatrixVarReductImplicit::N_ptr ( ) const

inline

Return the smart pointer to the aggregate nonbasis matrix object N.

If this is the only reference to this matrix object, then return.count() == 1 will be true.

Definition at line 291 of file ConstrainedOptPack_MatrixVarReductImplicit.hpp.

const MatrixVarReductImplicit::mat_ptr_t & ConstrainedOptPack::MatrixVarReductImplicit::D_direct_ptr ( ) const

inline

Return the smart pointer to the aggregate precomputed matrix object D_direct (if set).

If this is the only reference to this matrix object, then return.count() == 1 will be true.

Definition at line 298 of file ConstrainedOptPack_MatrixVarReductImplicit.hpp.

size_type ConstrainedOptPack::MatrixVarReductImplicit::rows ( ) const

virtual

Reimplemented from AbstractLinAlgPack::MatrixBase.

Definition at line 249 of file ConstrainedOptPack_MatrixVarReductImplicit.cpp.

size_type ConstrainedOptPack::MatrixVarReductImplicit::cols ( ) const

virtual

Reimplemented from AbstractLinAlgPack::MatrixBase.

Definition at line 254 of file ConstrainedOptPack_MatrixVarReductImplicit.cpp.

const VectorSpace & ConstrainedOptPack::MatrixVarReductImplicit::space_cols ( ) const

virtual

Implements AbstractLinAlgPack::MatrixBase.

Definition at line 261 of file ConstrainedOptPack_MatrixVarReductImplicit.cpp.

const VectorSpace & ConstrainedOptPack::MatrixVarReductImplicit::space_rows ( ) const

virtual

Implements AbstractLinAlgPack::MatrixBase.

Definition at line 267 of file ConstrainedOptPack_MatrixVarReductImplicit.cpp.

MatrixOp & ConstrainedOptPack::MatrixVarReductImplicit::operator= ( const MatrixOp & M )

Definition at line 273 of file ConstrainedOptPack_MatrixVarReductImplicit.cpp.

std::ostream & ConstrainedOptPack::MatrixVarReductImplicit::output ( std::ostream & o ) const

virtual

Reimplemented from AbstractLinAlgPack::MatrixOp.

Definition at line 280 of file ConstrainedOptPack_MatrixVarReductImplicit.cpp.

void ConstrainedOptPack::MatrixVarReductImplicit::Vp_StMtV	(	VectorMutable *	v_lhs,
		value_type	alpha,
		BLAS_Cpp::Transp	trans_rhs1,
		const Vector &	v_rhs2,
		value_type	beta
	)		const

Definition at line 289 of file ConstrainedOptPack_MatrixVarReductImplicit.cpp.

void ConstrainedOptPack::MatrixVarReductImplicit::Vp_StMtV	(	VectorMutable *	v_lhs,
		value_type	alpha,
		BLAS_Cpp::Transp	trans_rhs1,
		const SpVectorSlice &	sv_rhs2,
		value_type	beta
	)		const

Definition at line 300 of file ConstrainedOptPack_MatrixVarReductImplicit.cpp.

void ConstrainedOptPack::MatrixVarReductImplicit::Vp_StPtMtV	(	VectorMutable *	v_lhs,
		value_type	alpha,
		const GenPermMatrixSlice &	P_rhs1,
		BLAS_Cpp::Transp	P_rhs1_trans,
		BLAS_Cpp::Transp	M_rhs2_trans,
		const Vector &	v_rhs3,
		value_type	beta
	)		const

Definition at line 358 of file ConstrainedOptPack_MatrixVarReductImplicit.cpp.

void ConstrainedOptPack::MatrixVarReductImplicit::Vp_StPtMtV	(	VectorMutable *	v_lhs,
		value_type	alpha,
		const GenPermMatrixSlice &	P_rhs1,
		BLAS_Cpp::Transp	P_rhs1_trans,
		BLAS_Cpp::Transp	M_rhs2_trans,
		const SpVectorSlice &	sv_rhs3,
		value_type	beta
	)		const

Definition at line 388 of file ConstrainedOptPack_MatrixVarReductImplicit.cpp.

The documentation for this class was generated from the following files:

Public types

Constructors / initializers

Access

Overridden from MatrixBase.

Overridden from MatrixOp.

Detailed Description

Member Typedef Documentation

Member Function Documentation