Providing orthogonal polynomial calculus and interpolation, created by Spencer Sherwin, Aeronautics, Imperial College London, modified and redistributed by D. Ridzal. More...

#include <Intrepid_Polylib.hpp>

Static Public Member Functions
template<class Scalar >
static void	zwgj (Scalar z, Scalar w, const int np, const Scalar alpha, const Scalar beta)
	Gauss-Jacobi zeros and weights. More...

template<class Scalar >
static void	zwgrjm (Scalar z, Scalar w, const int np, const Scalar alpha, const Scalar beta)
	Gauss-Radau-Jacobi zeros and weights with end point at z=-1. More...

template<class Scalar >
static void	zwgrjp (Scalar z, Scalar w, const int np, const Scalar alpha, const Scalar beta)
	Gauss-Radau-Jacobi zeros and weights with end point at z=1. More...

template<class Scalar >
static void	zwglj (Scalar z, Scalar w, const int np, const Scalar alpha, const Scalar beta)
	Gauss-Lobatto-Jacobi zeros and weights with end point at z=-1,1. More...

template<class Scalar >
static void	Dgj (Scalar D, const Scalar z, const int np, const Scalar alpha, const Scalar beta)
	Compute the Derivative Matrix and its transpose associated with the Gauss-Jacobi zeros. More...

template<class Scalar >
static void	Dgrjm (Scalar D, const Scalar z, const int np, const Scalar alpha, const Scalar beta)
	Compute the Derivative Matrix and its transpose associated with the Gauss-Radau-Jacobi zeros with a zero at z=-1. More...

template<class Scalar >
static void	Dgrjp (Scalar D, const Scalar z, const int np, const Scalar alpha, const Scalar beta)
	Compute the Derivative Matrix associated with the Gauss-Radau-Jacobi zeros with a zero at z=1. More...

template<class Scalar >
static void	Dglj (Scalar D, const Scalar z, const int np, const Scalar alpha, const Scalar beta)
	Compute the Derivative Matrix associated with the Gauss-Lobatto-Jacobi zeros. More...

template<class Scalar >
static Scalar	hgj (const int i, const Scalar z, const Scalar *zgj, const int np, const Scalar alpha, const Scalar beta)
	Compute the value of the i th Lagrangian interpolant through the np Gauss-Jacobi points zgj at the arbitrary location z. More...

template<class Scalar >
static Scalar	hgrjm (const int i, const Scalar z, const Scalar *zgrj, const int np, const Scalar alpha, const Scalar beta)
	Compute the value of the i th Lagrangian interpolant through the np Gauss-Radau-Jacobi points zgrj at the arbitrary location z. This routine assumes zgrj includes the point -1. More...

template<class Scalar >
static Scalar	hgrjp (const int i, const Scalar z, const Scalar *zgrj, const int np, const Scalar alpha, const Scalar beta)
	Compute the value of the i th Lagrangian interpolant through the np Gauss-Radau-Jacobi points zgrj at the arbitrary location z. This routine assumes zgrj includes the point +1. More...

template<class Scalar >
static Scalar	hglj (const int i, const Scalar z, const Scalar *zglj, const int np, const Scalar alpha, const Scalar beta)
	Compute the value of the i th Lagrangian interpolant through the np Gauss-Lobatto-Jacobi points zglj at the arbitrary location z. More...

template<class Scalar >
static void	Imgj (Scalar im, const Scalar zgj, const Scalar *zm, const int nz, const int mz, const Scalar alpha, const Scalar beta)
	Interpolation Operator from Gauss-Jacobi points to an arbitrary distribution at points zm. More...

template<class Scalar >
static void	Imgrjm (Scalar im, const Scalar zgrj, const Scalar *zm, const int nz, const int mz, const Scalar alpha, const Scalar beta)
	Interpolation Operator from Gauss-Radau-Jacobi points (including z=-1) to an arbitrary distrubtion at points zm. More...

template<class Scalar >
static void	Imgrjp (Scalar im, const Scalar zgrj, const Scalar *zm, const int nz, const int mz, const Scalar alpha, const Scalar beta)
	Interpolation Operator from Gauss-Radau-Jacobi points (including z=1) to an arbitrary distrubtion at points zm. More...

template<class Scalar >
static void	Imglj (Scalar im, const Scalar zglj, const Scalar *zm, const int nz, const int mz, const Scalar alpha, const Scalar beta)
	Interpolation Operator from Gauss-Lobatto-Jacobi points to an arbitrary distrubtion at points zm. More...

template<class Scalar >
static void	jacobfd (const int np, const Scalar z, Scalar poly_in, Scalar *polyd, const int n, const Scalar alpha, const Scalar beta)
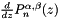	Routine to calculate Jacobi polynomials, $P^{\alpha,\beta}_n(z)$ , and their first derivative, $\frac{d}{dz} P^{\alpha,\beta}_n(z)$ . More...

template<class Scalar >
static void	jacobd (const int np, const Scalar z, Scalar polyd, const int n, const Scalar alpha, const Scalar beta)
	Calculate the derivative of Jacobi polynomials. More...

template<class Scalar >
static void	Jacobz (const int n, Scalar *z, const Scalar alpha, const Scalar beta)
	Calculate the n zeros, z, of the Jacobi polynomial, i.e. 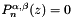$P_n^{\alpha,\beta}(z) = 0$ . More...

template<class Scalar >
static void	JacZeros (const int n, Scalar *a, const Scalar alpha, const Scalar beta)
	Zero determination through the eigenvalues of a tridiagonal matrix from the three term recursion relationship. More...

template<class Scalar >
static void	TriQL (const int n, Scalar d, Scalar e)
	QL algorithm for symmetric tridiagonal matrix. More...

template<class Scalar >
static Scalar	gammaF (const Scalar x)
	Calculate the Gamma function , 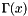$\Gamma(x)$ , for integer values x and halves. More...

Detailed Description

Providing orthogonal polynomial calculus and interpolation, created by Spencer Sherwin, Aeronautics, Imperial College London, modified and redistributed by D. Ridzal.

See original Polylib documentation.

Definition at line 223 of file Intrepid_Polylib.hpp.

Member Function Documentation

template<class Scalar >

void Intrepid::IntrepidPolylib::Dgj	(	Scalar *	D,
		const Scalar *	z,
		const int	np,
		const Scalar	alpha,
		const Scalar	beta
	)

static

Compute the Derivative Matrix and its transpose associated with the Gauss-Jacobi zeros.

Compute the derivative matrix D associated with the n_th order Lagrangian interpolants through the np Gauss-Jacobi points z such that
$\frac{du}{dz}(z[i]) = \sum_{j=0}^{np-1} D[i*np+j] u(z[j])$

Definition at line 210 of file Intrepid_PolylibDef.hpp.

References jacobd().

template<class Scalar >

void Intrepid::IntrepidPolylib::Dglj	(	Scalar *	D,
		const Scalar *	z,
		const int	np,
		const Scalar	alpha,
		const Scalar	beta
	)

static

Compute the Derivative Matrix associated with the Gauss-Lobatto-Jacobi zeros.

Compute the derivative matrix D associated with the n_th order Lagrange interpolants through the np Gauss-Lobatto-Jacobi points z such that
$\frac{du}{dz}(z[i]) = \sum_{j=0}^{np-1} D[i*np+j] u(z[j])$

Definition at line 324 of file Intrepid_PolylibDef.hpp.

References gammaF(), and jacobd().

template<class Scalar >

void Intrepid::IntrepidPolylib::Dgrjm	(	Scalar *	D,
		const Scalar *	z,
		const int	np,
		const Scalar	alpha,
		const Scalar	beta
	)

static

Compute the Derivative Matrix and its transpose associated with the Gauss-Radau-Jacobi zeros with a zero at z=-1.

Compute the derivative matrix D associated with the n_th order Lagrangian interpolants through the np Gauss-Radau-Jacobi points z such that
$\frac{du}{dz}(z[i]) = \sum_{j=0}^{np-1} D[i*np+j] u(z[j])$

Definition at line 243 of file Intrepid_PolylibDef.hpp.

References gammaF(), and jacobd().

template<class Scalar >

void Intrepid::IntrepidPolylib::Dgrjp	(	Scalar *	D,
		const Scalar *	z,
		const int	np,
		const Scalar	alpha,
		const Scalar	beta
	)

static

Compute the Derivative Matrix associated with the Gauss-Radau-Jacobi zeros with a zero at z=1.

Compute the derivative matrix D associated with the n_th order Lagrangian interpolants through the np Gauss-Radau-Jacobi points z such that
$\frac{du}{dz}(z[i]) = \sum_{j=0}^{np-1} D[i*np+j] u(z[j])$

Definition at line 283 of file Intrepid_PolylibDef.hpp.

References gammaF(), and jacobd().

template<class Scalar >

Scalar Intrepid::IntrepidPolylib::gammaF ( const Scalar x )

static

Calculate the Gamma function , 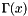$\Gamma(x)$ , for integer values x and halves.

Determine the value of 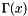$\Gamma(x)$ using:

$\Gamma(x) = (x-1)! \mbox{ or } \Gamma(x+1/2) = (x-1/2)\Gamma(x-1/2)$

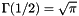
where $\Gamma(1/2) = \sqrt{\pi}$

Definition at line 810 of file Intrepid_PolylibDef.hpp.

Referenced by Dglj(), Dgrjm(), Dgrjp(), JacZeros(), zwgj(), zwglj(), zwgrjm(), and zwgrjp().

template<class Scalar >

Scalar Intrepid::IntrepidPolylib::hgj	(	const int	i,
		const Scalar	z,
		const Scalar *	zgj,
		const int	np,
		const Scalar	alpha,
		const Scalar	beta
	)

static

Compute the value of the i th Lagrangian interpolant through the np Gauss-Jacobi points zgj at the arbitrary location z.

$-1 \leq z \leq 1$

Uses the defintion of the Lagrangian interpolant:
$\begin{array}{rcl} h_j(z) = \left\{ \begin{array}{ll} \displaystyle \frac{P_{np}^{\alpha,\beta}(z)} {[P_{np}^{\alpha,\beta}(z_j)]^\prime (z-z_j)} & \mbox{if $z \ne z_j$}\\ & \\ 1 & \mbox{if $z=z_j$} \end{array} \right. \end{array}$

Definition at line 367 of file Intrepid_PolylibDef.hpp.

References jacobd(), and jacobfd().

Referenced by Imgj().

template<class Scalar >

Scalar Intrepid::IntrepidPolylib::hglj	(	const int	i,
		const Scalar	z,
		const Scalar *	zglj,
		const int	np,
		const Scalar	alpha,
		const Scalar	beta
	)

static

Compute the value of the i th Lagrangian interpolant through the np Gauss-Lobatto-Jacobi points zglj at the arbitrary location z.

$-1 \leq z \leq 1$

Uses the defintion of the Lagrangian interpolant:
% $\begin{array}{rcl} h_j(z) = \left\{ \begin{array}{ll} \displaystyle \frac{(1-z^2) P_{np-2}^{\alpha+1,\beta+1}(z)} {((1-z^2_j) [P_{np-2}^{\alpha+1,\beta+1}(z_j)]^\prime - 2 z_j P_{np-2}^{\alpha+1,\beta+1}(z_j) ) (z-z_j)}&\mbox{if $z \ne z_j$}\\ & \\ 1 & \mbox{if $z=z_j$} \end{array} \right. \end{array}$

Definition at line 430 of file Intrepid_PolylibDef.hpp.

References jacobd(), and jacobfd().

Referenced by Imglj().

template<class Scalar >

Scalar Intrepid::IntrepidPolylib::hgrjm	(	const int	i,
		const Scalar	z,
		const Scalar *	zgrj,
		const int	np,
		const Scalar	alpha,
		const Scalar	beta
	)

static

Compute the value of the i th Lagrangian interpolant through the np Gauss-Radau-Jacobi points zgrj at the arbitrary location z. This routine assumes zgrj includes the point -1.

$-1 \leq z \leq 1$

Uses the defintion of the Lagrangian interpolant:
% $\begin{array}{rcl} h_j(z) = \left\{ \begin{array}{ll} \displaystyle \frac{(1+z) P_{np-1}^{\alpha,\beta+1}(z)} {((1+z_j) [P_{np-1}^{\alpha,\beta+1}(z_j)]^\prime + P_{np-1}^{\alpha,\beta+1}(z_j) ) (z-z_j)} & \mbox{if $z \ne z_j$}\\ & \\ 1 & \mbox{if $z=z_j$} \end{array} \right. \end{array}$

Definition at line 386 of file Intrepid_PolylibDef.hpp.

References jacobd(), and jacobfd().

Referenced by Imgrjm().

template<class Scalar >

Scalar Intrepid::IntrepidPolylib::hgrjp	(	const int	i,
		const Scalar	z,
		const Scalar *	zgrj,
		const int	np,
		const Scalar	alpha,
		const Scalar	beta
	)

static

Compute the value of the i th Lagrangian interpolant through the np Gauss-Radau-Jacobi points zgrj at the arbitrary location z. This routine assumes zgrj includes the point +1.

$-1 \leq z \leq 1$

Uses the defintion of the Lagrangian interpolant:
% $\begin{array}{rcl} h_j(z) = \left\{ \begin{array}{ll} \displaystyle \frac{(1-z) P_{np-1}^{\alpha+1,\beta}(z)} {((1-z_j) [P_{np-1}^{\alpha+1,\beta}(z_j)]^\prime - P_{np-1}^{\alpha+1,\beta}(z_j) ) (z-z_j)} & \mbox{if $z \ne z_j$}\\ & \\ 1 & \mbox{if $z=z_j$} \end{array} \right. \end{array}$

Definition at line 408 of file Intrepid_PolylibDef.hpp.

References jacobd(), and jacobfd().

Referenced by Imgrjp().

template<class Scalar >

void Intrepid::IntrepidPolylib::Imgj	(	Scalar *	im,
		const Scalar *	zgj,
		const Scalar *	zm,
		const int	nz,
		const int	mz,
		const Scalar	alpha,
		const Scalar	beta
	)

static

Interpolation Operator from Gauss-Jacobi points to an arbitrary distribution at points zm.

Computes the one-dimensional interpolation matrix, im, to interpolate a function from at Gauss-Jacobi distribution of nz zeros zgj to an arbitrary distribution of mz points zm, i.e.
$u(zm[i]) = \sum_{j=0}^{nz-1} im[i*nz+j] \ u(zgj[j])$

Definition at line 452 of file Intrepid_PolylibDef.hpp.

References hgj().

template<class Scalar >

void Intrepid::IntrepidPolylib::Imglj	(	Scalar *	im,
		const Scalar *	zglj,
		const Scalar *	zm,
		const int	nz,
		const int	mz,
		const Scalar	alpha,
		const Scalar	beta
	)

static

Interpolation Operator from Gauss-Lobatto-Jacobi points to an arbitrary distrubtion at points zm.

Computes the one-dimensional interpolation matrix, im, to interpolate a function from at Gauss-Lobatto-Jacobi distribution of nz zeros zglj (where zglj[0]=-1 , zglj[nz-1]=1) to an arbitrary distribution of mz points zm, i.e.
$u(zm[i]) = \sum_{j=0}^{nz-1} im[i*nz+j] \ u(zglj[j])$

Definition at line 536 of file Intrepid_PolylibDef.hpp.

References hglj().

template<class Scalar >

void Intrepid::IntrepidPolylib::Imgrjm	(	Scalar *	im,
		const Scalar *	zgrj,
		const Scalar *	zm,
		const int	nz,
		const int	mz,
		const Scalar	alpha,
		const Scalar	beta
	)

static

Interpolation Operator from Gauss-Radau-Jacobi points (including z=-1) to an arbitrary distrubtion at points zm.

Computes the one-dimensional interpolation matrix, im, to interpolate a function from at Gauss-Radau-Jacobi distribution of nz zeros zgrj (where zgrj[0]=-1) to an arbitrary distribution of mz points zm, i.e.
$u(zm[i]) = \sum_{j=0}^{nz-1} im[i*nz+j] \ u(zgrj[j])$

Definition at line 480 of file Intrepid_PolylibDef.hpp.

References hgrjm().

template<class Scalar >

void Intrepid::IntrepidPolylib::Imgrjp	(	Scalar *	im,
		const Scalar *	zgrj,
		const Scalar *	zm,
		const int	nz,
		const int	mz,
		const Scalar	alpha,
		const Scalar	beta
	)

static

Interpolation Operator from Gauss-Radau-Jacobi points (including z=1) to an arbitrary distrubtion at points zm.

Computes the one-dimensional interpolation matrix, im, to interpolate a function from at Gauss-Radau-Jacobi distribution of nz zeros zgrj (where zgrj[nz-1]=1) to an arbitrary distribution of mz points zm, i.e.
$u(zm[i]) = \sum_{j=0}^{nz-1} im[i*nz+j] \ u(zgrj[j])$

Definition at line 508 of file Intrepid_PolylibDef.hpp.

References hgrjp().

template<class Scalar >

void Intrepid::IntrepidPolylib::jacobd	(	const int	np,
		const Scalar *	z,
		Scalar *	polyd,
		const int	n,
		const Scalar	alpha,
		const Scalar	beta
	)

static

Calculate the derivative of Jacobi polynomials.

Generates a vector poly of values of the derivative of the n-th order Jacobi polynomial 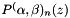$P^(\alpha,\beta)_n(z)$ at the np points z.

To do this we have used the relation
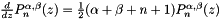
$\frac{d}{dz} P^{\alpha,\beta}_n(z) = \frac{1}{2} (\alpha + \beta + n + 1) P^{\alpha,\beta}_n(z)$

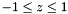
This formulation is valid for $-1 \leq z \leq 1$

Definition at line 657 of file Intrepid_PolylibDef.hpp.

References jacobfd().

Referenced by Dgj(), Dglj(), Dgrjm(), Dgrjp(), Intrepid::Basis_HGRAD_LINE_Cn_FEM_JACOBI< Scalar, ArrayScalar >::getValues(), hgj(), hglj(), hgrjm(), hgrjp(), and zwgj().

template<class Scalar >

void Intrepid::IntrepidPolylib::jacobfd	(	const int	np,
		const Scalar *	z,
		Scalar *	poly_in,
		Scalar *	polyd,
		const int	n,
		const Scalar	alpha,
		const Scalar	beta
	)

static

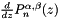Routine to calculate Jacobi polynomials, $P^{\alpha,\beta}_n(z)$ , and their first derivative, $\frac{d}{dz} P^{\alpha,\beta}_n(z)$ .

This function returns the vectors poly_in and poly_d containing the value of the n-th order Jacobi polynomial 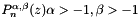$P^{\alpha,\beta}_n(z) \alpha > -1, \beta > -1$ and its derivative at the np points in z[i]

If poly_in = NULL then only calculate derivative
If polyd = NULL then only calculate polynomial
To calculate the polynomial this routine uses the recursion relationship (see appendix A ref [4]) : $\begin{array}{rcl} P^{\alpha,\beta}_0(z) &=& 1 \\ P^{\alpha,\beta}_1(z) &=& \frac{1}{2} [ \alpha-\beta+(\alpha+\beta+2)z] \\ a^1_n P^{\alpha,\beta}_{n+1}(z) &=& (a^2_n + a^3_n z) P^{\alpha,\beta}_n(z) - a^4_n P^{\alpha,\beta}_{n-1}(z) \\ a^1_n &=& 2(n+1)(n+\alpha + \beta + 1)(2n + \alpha + \beta) \\ a^2_n &=& (2n + \alpha + \beta + 1)(\alpha^2 - \beta^2) \\ a^3_n &=& (2n + \alpha + \beta)(2n + \alpha + \beta + 1) (2n + \alpha + \beta + 2) \\ a^4_n &=& 2(n+\alpha)(n+\beta)(2n + \alpha + \beta + 2) \end{array}$
To calculate the derivative of the polynomial this routine uses the relationship (see appendix A ref [4]) : $\begin{array}{rcl} b^1_n(z)\frac{d}{dz} P^{\alpha,\beta}_n(z)&=&b^2_n(z)P^{\alpha,\beta}_n(z) + b^3_n(z) P^{\alpha,\beta}_{n-1}(z) \hspace{2.2cm} \\ b^1_n(z) &=& (2n+\alpha + \beta)(1-z^2) \\ b^2_n(z) &=& n[\alpha - \beta - (2n+\alpha + \beta)z]\\ b^3_n(z) &=& 2(n+\alpha)(n+\beta) \end{array}$
Note the derivative from this routine is only valid for -1 < z < 1.

Definition at line 566 of file Intrepid_PolylibDef.hpp.

Referenced by Intrepid::Basis_HGRAD_LINE_Cn_FEM_JACOBI< Scalar, ArrayScalar >::getValues(), hgj(), hglj(), hgrjm(), hgrjp(), jacobd(), Jacobz(), zwglj(), zwgrjm(), and zwgrjp().

template<class Scalar >

void Intrepid::IntrepidPolylib::Jacobz	(	const int	n,
		Scalar *	z,
		const Scalar	alpha,
		const Scalar	beta
	)

static

Calculate the n zeros, z, of the Jacobi polynomial, i.e. 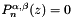$P_n^{\alpha,\beta}(z) = 0$ .

This routine is only valid for 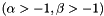$( \alpha > -1, \beta > -1)$ and uses polynomial deflation in a Newton iteration

Definition at line 674 of file Intrepid_PolylibDef.hpp.

References INTREPID_POLYLIB_STOP, and jacobfd().

template<class Scalar >

void Intrepid::IntrepidPolylib::JacZeros	(	const int	n,
		Scalar *	a,
		const Scalar	alpha,
		const Scalar	beta
	)

static

Zero determination through the eigenvalues of a tridiagonal matrix from the three term recursion relationship.

Set up a symmetric tridiagonal matrix

$\left [ \begin{array}{ccccc} a[0] & b[0] & & & \\ b[0] & a[1] & b[1] & & \\ 0 & \ddots & \ddots & \ddots & \\ & & \ddots & \ddots & b[n-2] \\ & & & b[n-2] & a[n-1] \end{array} \right ]$

Where the coefficients a[n], b[n] come from the recurrence relation

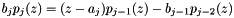
$b_j p_j(z) = (z - a_j ) p_{j-1}(z) - b_{j-1} p_{j-2}(z)$

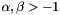where $ j=n+1$ and $p_j(z)$ are the Jacobi (normalized) orthogonal polynomials $\alpha,\beta > -1$ ( integer values and halves). Since the polynomials are orthonormalized, the tridiagonal matrix is guaranteed to be symmetric. The eigenvalues of this matrix are the zeros of the Jacobi polynomial.

Definition at line 705 of file Intrepid_PolylibDef.hpp.

References gammaF(), and TriQL().

template<class Scalar >

void Intrepid::IntrepidPolylib::TriQL	(	const int	n,
		Scalar *	d,
		Scalar *	e
	)

static

QL algorithm for symmetric tridiagonal matrix.

This subroutine is a translation of an algol procedure, num. math. 12, 377-383(1968) by martin and wilkinson, as modified in num. math. 15, 450(1970) by dubrulle. Handbook for auto. comp., vol.ii-linear algebra, 241-248(1971). This is a modified version from numerical recipes.

This subroutine finds the eigenvalues and first components of the eigenvectors of a symmetric tridiagonal matrix by the implicit QL method.

on input:

n is the order of the matrix;
d contains the diagonal elements of the input matrix;
e contains the subdiagonal elements of the input matrix in its first n-1 positions. e(n) is arbitrary;

on output:

d contains the eigenvalues in ascending order.
e has been destroyed;

Definition at line 744 of file Intrepid_PolylibDef.hpp.

Referenced by JacZeros().

template<class Scalar >

void Intrepid::IntrepidPolylib::zwgj	(	Scalar *	z,
		Scalar *	w,
		const int	np,
		const Scalar	alpha,
		const Scalar	beta
	)

static

Gauss-Jacobi zeros and weights.

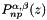Generate np Gauss Jacobi zeros, z, and weights,w, associated with the Jacobi polynomial $P^{\alpha,\beta}_{np}(z)$ ,

Exact for polynomials of order 2np-1 or less

Definition at line 113 of file Intrepid_PolylibDef.hpp.

References gammaF(), jacobd(), and jacobz.

Referenced by Intrepid::CubaturePolylib< Scalar, ArrayPoint, ArrayWeight >::getCubature(), and Intrepid::PointTools::getGaussPoints().

template<class Scalar >

void Intrepid::IntrepidPolylib::zwglj	(	Scalar *	z,
		Scalar *	w,
		const int	np,
		const Scalar	alpha,
		const Scalar	beta
	)

static

Gauss-Lobatto-Jacobi zeros and weights with end point at z=-1,1.

Generate np Gauss-Lobatto-Jacobi points, z, and weights, w, associated with polynomial $(1-z)(1+z) P^{\alpha+1,\beta+1}_{np-2}(z)$

Exact for polynomials of order 2np-3 or less

Definition at line 182 of file Intrepid_PolylibDef.hpp.

References gammaF(), jacobfd(), and jacobz.

Referenced by Intrepid::CubaturePolylib< Scalar, ArrayPoint, ArrayWeight >::getCubature(), and Intrepid::PointTools::getWarpBlendLatticeLine().

template<class Scalar >

void Intrepid::IntrepidPolylib::zwgrjm	(	Scalar *	z,
		Scalar *	w,
		const int	np,
		const Scalar	alpha,
		const Scalar	beta
	)

static

Gauss-Radau-Jacobi zeros and weights with end point at z=-1.

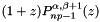Generate np Gauss-Radau-Jacobi zeros, z, and weights,w, associated with the polynomial $(1+z) P^{\alpha,\beta+1}_{np-1}(z)$ .

Exact for polynomials of order 2np-2 or less

Definition at line 130 of file Intrepid_PolylibDef.hpp.

References gammaF(), jacobfd(), and jacobz.

Referenced by Intrepid::CubaturePolylib< Scalar, ArrayPoint, ArrayWeight >::getCubature().

template<class Scalar >

void Intrepid::IntrepidPolylib::zwgrjp	(	Scalar *	z,
		Scalar *	w,
		const int	np,
		const Scalar	alpha,
		const Scalar	beta
	)

static

Gauss-Radau-Jacobi zeros and weights with end point at z=1.

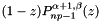Generate np Gauss-Radau-Jacobi zeros, z, and weights,w, associated with the polynomial $(1-z) P^{\alpha+1,\beta}_{np-1}(z)$ .

Exact for polynomials of order 2np-2 or less

Definition at line 156 of file Intrepid_PolylibDef.hpp.

References gammaF(), jacobfd(), and jacobz.

Referenced by Intrepid::CubaturePolylib< Scalar, ArrayPoint, ArrayWeight >::getCubature().

The documentation for this class was generated from the following files:

http://docs.trilinos.org/dev/packages/intrepid/src/Shared/Intrepid_Polylib.hpp
http://docs.trilinos.org/dev/packages/intrepid/src/Shared/Intrepid_PolylibDef.hpp

Static Public Member Functions

Detailed Description

Member Function Documentation