Implements Hermite interpolant basis of degree n on the reference Line cell. The basis has cardinality 2n and spans a COMPLETE linear polynomial space. More...
#include <Intrepid_HGRAD_LINE_Hermite_FEM.hpp>
Public Member Functions | |
| Basis_HGRAD_LINE_Hermite_FEM () | |
| Default Constructor assumes the two interpolation points are the cell vertices. Cubic Hermite Interpolation. | |
| Basis_HGRAD_LINE_Hermite_FEM (const ArrayScalar &pts) | |
| Constructor. More... | |
| Basis_HGRAD_LINE_Hermite_FEM (int numPoints, const EPointType &pointType) | |
| Constructor. More... | |
| void | getValues (ArrayScalar &outputValues, const ArrayScalar &inputPoints, const EOperator operatorType) const |
| Evaluation of a FEM basis on a reference Line cell. More... | |
| void | getValues (ArrayScalar &outputValues, const ArrayScalar &inputPoints, const ArrayScalar &cellVertices, const EOperator operatorType=OPERATOR_VALUE) const |
| FVD basis evaluation: invocation of this method throws an exception. | |
| virtual void | getDofCoords (ArrayScalar &DofCoords) const |
| implements the dofcoords interface | |
| void | printTags (std::ostream &os) |
 Public Member Functions inherited from Intrepid::Basis< Scalar, ArrayScalar > Public Member Functions inherited from Intrepid::Basis< Scalar, ArrayScalar > | |
| virtual | ~Basis () |
| Destructor. | |
| virtual int | getCardinality () const |
| Returns cardinality of the basis. More... | |
| virtual int | getDegree () const |
| Returns the degree of the basis. More... | |
| virtual const shards::CellTopology | getBaseCellTopology () const |
| Returns the base cell topology for which the basis is defined. See Shards documentation http://trilinos.sandia.gov/packages/shards for definition of base cell topology. More... | |
| virtual EBasis | getBasisType () const |
| Returns the basis type. More... | |
| virtual ECoordinates | getCoordinateSystem () const |
| Returns the type of coordinate system for which the basis is defined. More... | |
| virtual int | getDofOrdinal (const int subcDim, const int subcOrd, const int subcDofOrd) |
| DoF tag to ordinal lookup. More... | |
|
virtual const std::vector < std::vector< std::vector < int > > > & | getDofOrdinalData () |
| DoF tag to ordinal data structure. | |
| virtual const std::vector< int > & | getDofTag (const int dofOrd) |
| DoF ordinal to DoF tag lookup. More... | |
| virtual const std::vector < std::vector< int > > & | getAllDofTags () |
| Retrieves all DoF tags. More... | |
Private Types | |
| template<typename T > | |
| using | RCP = Teuchos::RCP< T > |
| using | SerialDenseMatrix = Teuchos::SerialDenseMatrix< int, Scalar > |
| using | TAGS = std::vector< int > |
Private Member Functions | |
| void | initializeTags () |
| Initializes tagToOrdinal_ and ordinalToTag_ lookup arrays. | |
| void | recurrence (ArrayScalar &P, ArrayScalar &Px, const Scalar x) const |
Evaluates 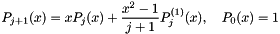 and and 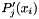 at a particular point at a particular point 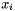 . . | |
| void | legendre_d (ArrayScalar &Pm, ArrayScalar &Pm1, const int m, const Scalar pt) const |
Evaluates 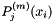 and and 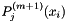 at a particular point at a particular point 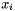 . . | |
| void | setupVandermonde (bool factor=true) |
| Form the Legendre/Derivative Vandermonde matrix at the given lattice points and have the linear solver factor with equilibration. | |
Private Attributes | |
| FieldContainer< Scalar > | latticePts_ |
| Holds the points defining the Hermite basis. | |
| SerialDenseMatrix | V_ |
| Contains the values of the Legendre polynomials and their derivatives. | |
|
Teuchos::SerialDenseSolver < int, Scalar > | solver_ |
| TAGS | tags_ |
| bool | isFactored_ |
Additional Inherited Members | |
 Protected Attributes inherited from Intrepid::Basis< Scalar, ArrayScalar > Protected Attributes inherited from Intrepid::Basis< Scalar, ArrayScalar > | |
| int | basisCardinality_ |
| Cardinality of the basis, i.e., the number of basis functions/degrees-of-freedom. | |
| int | basisDegree_ |
| Degree of the largest complete polynomial space that can be represented by the basis. | |
| shards::CellTopology | basisCellTopology_ |
| Base topology of the cells for which the basis is defined. See the Shards package http://trilinos.sandia.gov/packages/shards for definition of base cell topology. | |
| EBasis | basisType_ |
| Type of the basis. | |
| ECoordinates | basisCoordinates_ |
| The coordinate system for which the basis is defined. | |
| bool | basisTagsAreSet_ |
| "true" if tagToOrdinal_ and ordinalToTag_ have been initialized | |
| std::vector< std::vector< int > > | ordinalToTag_ |
| DoF ordinal to tag lookup table. More... | |
| std::vector< std::vector < std::vector< int > > > | tagToOrdinal_ |
| DoF tag to ordinal lookup table. More... | |
Detailed Description
template<class Scalar, class ArrayScalar>
class Intrepid::Basis_HGRAD_LINE_Hermite_FEM< Scalar, ArrayScalar >
Implements Hermite interpolant basis of degree n on the reference Line cell. The basis has cardinality 2n and spans a COMPLETE linear polynomial space.
The Hermite interpolant approximation space is \form#395 where \form#396
![\[\mathcal{H}_n = \{h_{2j}(x),h_{2j+1}\}_{j=0}^{n-1} \]](form_397.png)
The basis functions determined by the interpolation points \form#409 which satisfy the ordering property
![\[ -1\leq x_0 \leq \cdots \leq x_i \leq x_{i+1} \leq \cdots \leq x_n \leq 1 \]](form_399.png)
while the basis functions satisfy
![\[ h_{2j}(x_i) = \delta_{ij},\quad h'_{2j}(x_i) = 0 \]](form_400.png)
![\[ h_{2j+1}(x_i) = 0,\quad h'_{2j+1}(x_i) = \delta_{ij} \]](form_401.png)
Basis functions and their derivatives are evaluated from the Legendre polynomials and their derivatives evaluated on the interpolation points and the input points in the getValues() method. Legendre polynomials and their derivatives are computed using the relations
![\[ P_{j+1}(x) = x P_j(x) + \frac{x^2-1}{j+1}P_j^{(1)}(x),\quad P_0(x) = 1 \]](form_402.png)
![\[ P_{j+1}^{(m)(x)} = (j+m)P_j^{(m-1)}(x) + x P_j^{(m)}(x),\quad P_j^{(m)} = 0,\;\forall j<m\]](form_410.png)
Definition at line 93 of file Intrepid_HGRAD_LINE_Hermite_FEM.hpp.
Constructor & Destructor Documentation
| Intrepid::Basis_HGRAD_LINE_Hermite_FEM< Scalar, ArrayScalar >::Basis_HGRAD_LINE_Hermite_FEM | ( | const ArrayScalar & | pts | ) |
Constructor.
- Parameters
-
int pointType: [in] array containing interpolation points
Definition at line 80 of file Intrepid_HGRAD_LINE_Hermite_FEMDef.hpp.
References Intrepid::Basis< Scalar, ArrayScalar >::basisCardinality_, Intrepid::Basis< Scalar, ArrayScalar >::basisCellTopology_, Intrepid::Basis< Scalar, ArrayScalar >::basisCoordinates_, Intrepid::Basis< Scalar, ArrayScalar >::basisDegree_, Intrepid::Basis< Scalar, ArrayScalar >::basisTagsAreSet_, Intrepid::Basis< Scalar, ArrayScalar >::basisType_, Intrepid::Basis_HGRAD_LINE_Hermite_FEM< Scalar, ArrayScalar >::latticePts_, and Intrepid::Basis_HGRAD_LINE_Hermite_FEM< Scalar, ArrayScalar >::setupVandermonde().
| Intrepid::Basis_HGRAD_LINE_Hermite_FEM< Scalar, ArrayScalar >::Basis_HGRAD_LINE_Hermite_FEM | ( | int | numPoints, |
| const EPointType & | pointType | ||
| ) |
Constructor.
- Parameters
-
int numPoints: [in] number of interpolation points int pointType: [in] type of points, either POINTTYPE_EQUISPACED or POINTTYPE_SPECTRAL
Definition at line 121 of file Intrepid_HGRAD_LINE_Hermite_FEMDef.hpp.
References Intrepid::Basis< Scalar, ArrayScalar >::basisCardinality_, Intrepid::Basis< Scalar, ArrayScalar >::basisCellTopology_, Intrepid::Basis< Scalar, ArrayScalar >::basisCoordinates_, Intrepid::Basis< Scalar, ArrayScalar >::basisDegree_, Intrepid::Basis< Scalar, ArrayScalar >::basisTagsAreSet_, Intrepid::Basis< Scalar, ArrayScalar >::basisType_, Intrepid::Basis_HGRAD_LINE_Hermite_FEM< Scalar, ArrayScalar >::latticePts_, and Intrepid::Basis_HGRAD_LINE_Hermite_FEM< Scalar, ArrayScalar >::setupVandermonde().
Member Function Documentation
|
virtual |
Evaluation of a FEM basis on a reference Line cell.
Returns values of <var>operatorType</var> acting on FEM basis functions for a set of
points in the <strong>reference Line</strong> cell. For rank and dimensions of
I/O array arguments see Section \ref basis_md_array_sec .
- Parameters
-
outputValues [out] - variable rank array with the basis values inputPoints [in] - rank-n array (P,D) with the evaluation points operatorType [in] - the operator acting on the basis functions
Implements Intrepid::Basis< Scalar, ArrayScalar >.
Definition at line 252 of file Intrepid_HGRAD_LINE_Hermite_FEMDef.hpp.
The documentation for this class was generated from the following files:
- http://docs.trilinos.org/dev/packages/intrepid/src/Discretization/Basis/Intrepid_HGRAD_LINE_Hermite_FEM.hpp
- http://docs.trilinos.org/dev/packages/intrepid/src/Discretization/Basis/Intrepid_HGRAD_LINE_Hermite_FEMDef.hpp
 1.8.5
1.8.5