|
Belos Package Browser (Single Doxygen Collection)
Development
|
|
Belos Package Browser (Single Doxygen Collection)
Development
|
Inner solver interface. More...
#include <BelosInnerSolver.hpp>
Public Types | |
| typedef Scalar | scalar_type |
| typedef Teuchos::ScalarTraits < Scalar >::magnitudeType | magnitude_type |
| typedef MV | multivector_type |
| typedef OP | operator_type |
Public Member Functions | |
| virtual | ~InnerSolver () |
| Virtual destructor, for correctness. More... | |
| virtual Teuchos::RCP< const Teuchos::ParameterList > | getCurrentParameters () const =0 |
| Current parameters for the inner solver implementation. More... | |
| virtual InnerSolveResult | solve (const Teuchos::RCP< MV > &X, const Teuchos::RCP< const MV > &B, const magnitude_type convTol, const int maxItersPerRestart, const int maxNumRestarts)=0 |
Solve 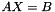 for the given right-hand side(s) B. More... for the given right-hand side(s) B. More... | |
| virtual InnerSolveResult | solve (const Teuchos::RCP< MV > &X, const Teuchos::RCP< const MV > &B)=0 |
Solve 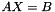 for the given right-hand side(s) B. More... for the given right-hand side(s) B. More... | |
Inner solver interface.
An "inner solver" wraps an existing linear solver, especially an iterative solver (such as any of the iterative solvers implemented in Belos). InnerSolver is designed especially for implementing the inner solve in inner-outer iterations, such as the following:
InnerSolvers may be used directly as the "OP" template argument in Belos::OperatorTraits, but Belos' current architecture makes this hard to use in practice. The more typical use is via the wrapper defined in Belos::InnerSolveTraits. The InnerSolveTraits::makeInnerSolveOperator() method wraps an InnerSolve instance in an operator appropriate for your linear algebra library: Epetra_Operator for Epetra, Tpetra::Operator for Tpetra, or Thyra::LinearOpBase for Thyra. Then, you can mix and match InnerSolver instances with ordinary matrices or other kinds of operators in your Belos iterative solvers. The wrappers have an "envelope" capability, so your custom iterative solvers can receive the InnerSolver wrapped up in the wrapper, extract the InnerSolver (via Belos::InnerSolveTraits::getInnerSolver()), discard the wrapper if desired, and use the InnerSolver directly.
Definition at line 106 of file BelosInnerSolver.hpp.
| typedef Scalar Belos::InnerSolver< Scalar, MV, OP >::scalar_type |
Definition at line 108 of file BelosInnerSolver.hpp.
| typedef Teuchos::ScalarTraits<Scalar>::magnitudeType Belos::InnerSolver< Scalar, MV, OP >::magnitude_type |
Definition at line 109 of file BelosInnerSolver.hpp.
| typedef MV Belos::InnerSolver< Scalar, MV, OP >::multivector_type |
Definition at line 110 of file BelosInnerSolver.hpp.
| typedef OP Belos::InnerSolver< Scalar, MV, OP >::operator_type |
Definition at line 111 of file BelosInnerSolver.hpp.
|
inlinevirtual |
Virtual destructor, for correctness.
Definition at line 114 of file BelosInnerSolver.hpp.
|
pure virtual |
Current parameters for the inner solver implementation.
These parameters may change values in place, if the five-argument version of the solve() method is called. If you want to preserve the original parameter values, make a deep copy of the returned ParameterList.
|
pure virtual |
Solve 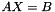 for the given right-hand side(s) B.
for the given right-hand side(s) B.
Implementations are free to interpret the convergence tolerance and maximum iteration count parameters in any way they please. (They should interpret these parameters consistently between calls.) They are also free to preserve more state between calls than just the matrix and preconditioner(s); for example, they may choose to perform Krylov subspace recycling.
| X | [in/out] On input: The initial guess for the inner solver, if the inner solver accepts an initial guess (it is not required to do so). On output: the approximate solution to Ax=B as computed by the inner solver. Whether or not the solver accepts an initial guess, X must be allocated to hold the output, and it must be in the range vector space of this solver. |
| B | [in] Right-hand side(s) for which to solve. It must be in the domain vector space of this solver. |
| convTol | [in] "Convergence tolerance," the meaning of which depends on the subclass |
| maxItersPerRestart | [in] Maximum number of iterations per restart cycle in the inner solve. |
| maxNumRestarts | [in] Maximum number of restart cycle(s) in the inner solve. |
solve() may not be a pure function. For example, if the inner solve implementation is a recycling Krylov solver, it may compute a different (hopefully better) approximate solution if given the same inputs twice in a row, or at least it may converge in fewer iterations the second time.
|
pure virtual |
Solve 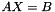 for the given right-hand side(s) B.
for the given right-hand side(s) B.
This should do the same thing as the five-argument version of solve(), except it should pick reasonable defaults for the convergence tolerance, maximum number of iterations, and maximum number of restart cycles.
| X | [in/out] On input: The initial guess for the inner solver, if the inner solver accepts an initial guess (it is not required to do so). On output: the approximate solution to Ax=B as computed by the inner solver. Whether or not the solver accepts an initial guess, X must be allocated to hold the output, and it must be in the range vector space of this solver. |
| B | [in] Right-hand side(s) for which to solve. It must be in the domain vector space of this solver. |
solve() may not be a pure function. For example, if the inner solve implementation is a recycling Krylov solver, it may compute a different (hopefully better) approximate solution if given the same inputs twice in a row, or at least it may converge in fewer iterations the second time. Third, the two-argument version of solve() reserves the right to modify the stopping criteria on each call.  1.8.5
1.8.5