|
Aristos
Development
|
Implements a trust-region (TR) sequential quadratic programming (SQP) algorithm for equality-constrained optimization. More...
#include <Aristos_SQPAlgoDecl.hpp>
Public Member Functions | |
| SQPAlgo (DataPool &dat, Objective &obj, Constraints &constr, HessVec &hessvec, LagMult &lagmult, FeasStep &feasstep) | |
| bool | run (Vector &x, Vector &c, Vector &l, int &iter, int &iflag, Teuchos::ParameterList &parlist) |
| Runs the trust-region SQP algorithm. More... | |
| bool | runMultiplierEst (const Vector &x, const Vector &g, Vector &l, double tol) |
| Computes a Lagrange multiplier estimate. More... | |
| bool | runQuasiNormalStep (const Vector &x, const Vector &c, Vector &s, double delta, double tol) |
| Computes the quasi-normal step. More... | |
| bool | runTangentialStep (const Vector &x, const Vector &g, const Vector &v, const Vector &l, Vector &s, double delta, int cgitmax, double cgtol, double tol, int &cgiter, int &iflag) |
| Computes the tangential step. More... | |
| bool | runTangentialStepInx (const Vector &x, const Vector &g, const Vector &v, const Vector &l, Vector &s, double delta, int cgitmax, double cgtol, double fixedtol, bool istolfixed, bool fullortho, bool orthocheck, bool fcdcheck, int &cgiter, int &iflag) |
| Computes the tangential step using the inexact CG algorithm with full orthogonalization and inexactness control. More... | |
| bool | runAcceptStep (Vector &x, const Vector &l, double f, const Vector &g, const Vector &c, const Vector &v, const Vector &w, double &delta, double &rho, double tol, int &iaccept) |
| Checks whether the computed step is acceptable, and accordingly updates the trust-region radius and the merit function penalty parameter. More... | |
| bool | runAcceptStepInx (Vector &x, const Vector &l, double f, const Vector &g, const Vector &c, const Vector &v, Vector &w, double &delta, double &rho, bool addproj, double &projtol, double tol, int &iaccept) |
| Checks whether the computed step is acceptable, and accordingly updates the trust-region radius and the merit function penalty parameter. Should be used whenever the SQP algorithm manages inexactness in linear system solves. More... | |
| bool | runDerivativeCheck (const Vector &x, const Vector &l, const Vector &dir) |
| Derivative checks.. More... | |
Implements a trust-region (TR) sequential quadratic programming (SQP) algorithm for equality-constrained optimization.
Aristos::SQPAlgo solves equality-constrained nonlinear optimization problems of the type:
![\[ \min f(x) \]](form_4.png)
![\[ \mbox{subject to } c(x) = 0 \]](form_5.png)
where \form#6, \form#7, and \form#8 and \form#9 are Hilbert spaces. We utilize a trust-region SQP approach in which the quadratic subproblems are solved using a composite step strategy. The TR quadratic subproblems are of the form
![\[ \min \frac{1}{2} \langle H_k s^x_k, s^x_k \rangle_{\mathcal{X}} + \langle \nabla_x \mathcal{L} (x_k, \lambda_k), s^x_k \rangle_{\mathcal{X}} \]](form_10.png)
subject to
![\[ c_x(x_k)s^x_k + c(x_k) = 0 \]](form_11.png)
![\[ \|s^x_k\|_{\mathcal{X}} \le \Delta_k \]](form_12.png)
where  is the Lagrangian functional with multipliers
is the Lagrangian functional with multipliers 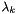 ,
, 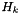 is a representation of the Hessian of the Lagrangian at
is a representation of the Hessian of the Lagrangian at 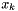 , and
, and  is the trust-region radius at iteration
is the trust-region radius at iteration 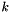 . The step
. The step 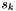 consists of a quasi-normal step that moves the model toward feasibility and a tangential step that moves the model toward optimality while staying in the null space of the linearized constraints (at least in absence of inexact linear system solves). Based on this approach, the SQP algorithm consists of the following steps:
consists of a quasi-normal step that moves the model toward feasibility and a tangential step that moves the model toward optimality while staying in the null space of the linearized constraints (at least in absence of inexact linear system solves). Based on this approach, the SQP algorithm consists of the following steps:
| bool Aristos::SQPAlgo::run | ( | Vector & | x, |
| Vector & | c, | ||
| Vector & | l, | ||
| int & | iter, | ||
| int & | iflag, | ||
| Teuchos::ParameterList & | parlist | ||
| ) |
Runs the trust-region SQP algorithm.
| x | [in,out] - Initial SQP iterate vector, final solution vector. |
| c | [out] - The vector of constraint values. |
| l | [out] - The vector of Lagrange multipliers. |
| iter | [out] - Total number of SQP iterations. |
| iflag | [out] - Return code: if 0, the algorithm has converged to desired tolerances within the maximum number of iterations; if 1, the maximum number of iterations has been exceeded; if 2, the trust-region radius has fallen below its allowed minimum. |
| parlist | [in] - Parameter list. |
true if the SQP run is successful.The SQP algorithm consists of the following steps:
Please read the documentation provided for the corresponding member functions.
References Aristos::Vector::createVector(), Aristos::Vector::innerProd(), runAcceptStepInx(), runMultiplierEst(), runQuasiNormalStep(), and runTangentialStepInx().
| bool Aristos::SQPAlgo::runAcceptStep | ( | Vector & | x, |
| const Vector & | l, | ||
| double | f, | ||
| const Vector & | g, | ||
| const Vector & | c, | ||
| const Vector & | v, | ||
| const Vector & | w, | ||
| double & | delta, | ||
| double & | rho, | ||
| double | tol, | ||
| int & | iaccept | ||
| ) |
Checks whether the computed step is acceptable, and accordingly updates the trust-region radius and the merit function penalty parameter.
| x | [in,out] - SQP iterate. |
| l | [in] - Current Lagrange multiplier estimate. |
| f | [in] - Current value of the objective. |
| g | [in] - Current gradient of the objective vector. |
| c | [in] - The vector of constraint values. |
| v | [in] - Current quasi-normal step. |
| w | [in] - Current tangential step. |
| s | [out] - The computed tangential step vector. |
| delta | [in,out] - Trust-region radius. |
| rho | [in,out] - Penalty parameter. |
| tol | [in] - Tolerance for inexact computations. |
| iaccept | [out] - Integer return code: 0 - step rejected 1 - step accepted |
true if runTangentialStep terminates successfully.Global convergence in trust-region SQP methods is usually ensured through the use of a merit function, which helps us determine whether a step is acceptable and whether the trust-region radius needs to be modified. We use the augmented Lagrangian merit function
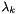
Let  be a trial step where
be a trial step where 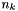 is the computed quasi-normal step, and
is the computed quasi-normal step, and 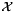 is the computed tangential step, and let
is the computed tangential step, and let 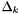 be an updated Lagrange multiplier. To measure the improvement in the merit function
be an updated Lagrange multiplier. To measure the improvement in the merit function 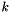 , we compare the actual reduction and the predicted reduction in moving from the current iterate
, we compare the actual reduction and the predicted reduction in moving from the current iterate 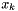 to the trial iterate
to the trial iterate 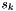 . The actual reduction is defined by
. The actual reduction is defined by
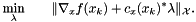
and the predicted reduction is given by
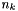
where
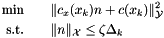
The following decision procedure is then used (we leave out the details of the penalty parameter update):
![\begin{enumerate} \addtocounter{enumi}{-1} \item Assume $0 < \eta_1 < \eta_2 < 1$, $0 < \gamma_1 < \gamma_2 < 1$. \item Acceptance Test. \begin{enumerate} \item Update penalty parameter $\rho_k$ (details omitted). \item Compute actual reduction $ared(s_k^x; \rho_k)$ and predicted reduction $pred(s_k^x; \rho_k)$, and their ratio $\theta_k=\frac{ared(s_k^x; \rho_k)}{pred(s_k^x; \rho_k)}$. \item If $\theta_k \ge \eta_1$, set $x_{k+1} = x_k+s_k$, otherwise set $x_{k+1} = x_k$ and reset $\lambda_{k+1} = \lambda_k$. \end{enumerate} \item Trust-Region Radius Update. Set \[ \Delta_{k+1} \in \begin{cases} [ \Delta_k, \infty] & \mbox{ if } \; \theta_k \ge \eta_2, \\ [ \gamma_2 \Delta_k, \Delta_k ] & \mbox{ if } \; \theta_k \in [\eta_1, \eta_2), \\ [ \gamma_1 \Delta_k, \gamma_2 \Delta_k ] & \mbox{ if } \; \theta_k < \eta_1. \end{cases} \] \end{enumerate}](form_46.png)
References Aristos::Vector::createVector(), Aristos::Vector::innerProd(), Aristos::Vector::linComb(), and runMultiplierEst().
| bool Aristos::SQPAlgo::runAcceptStepInx | ( | Vector & | x, |
| const Vector & | l, | ||
| double | f, | ||
| const Vector & | g, | ||
| const Vector & | c, | ||
| const Vector & | v, | ||
| Vector & | w, | ||
| double & | delta, | ||
| double & | rho, | ||
| bool | addproj, | ||
| double & | projtol, | ||
| double | tol, | ||
| int & | iaccept | ||
| ) |
Checks whether the computed step is acceptable, and accordingly updates the trust-region radius and the merit function penalty parameter. Should be used whenever the SQP algorithm manages inexactness in linear system solves.
| x | [in,out] - SQP iterate. |
| l | [in] - Current Lagrange multiplier estimate. |
| f | [in] - Current value of the objective. |
| g | [in] - Current gradient of the objective vector. |
| c | [in] - The vector of constraint values. |
| v | [in] - Current quasi-normal step. |
| w | [in] - Current tangential step. |
| s | [out] - The computed tangential step vector. |
| delta | [in,out] - Trust-region radius. |
| rho | [in,out] - Penalty parameter. |
| addproj[in] | - if true, run an additional null-space projection |
| projtol[in,out] | - Tolerance for inexact null-space projections. |
| tol | [in] - Tolerance for inexact derivative, etc computations. |
| iaccept | [out] - Integer return code: 0 - step rejected 1 - step accepted |
true if runTangentialStepInx terminates successfully.Global convergence in trust-region SQP methods is usually ensured through the use of a merit function, which helps us determine whether a step is acceptable and whether the trust-region radius needs to be modified. We use the augmented Lagrangian merit function
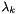
Let  be a trial step where
be a trial step where 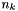 is the computed quasi-normal step, and
is the computed quasi-normal step, and 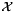 is the computed tangential step, and let
is the computed tangential step, and let 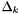 be an updated Lagrange multiplier. To measure the improvement in the merit function
be an updated Lagrange multiplier. To measure the improvement in the merit function 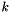 , we compare the actual reduction and the predicted reduction in moving from the current iterate
, we compare the actual reduction and the predicted reduction in moving from the current iterate 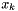 to the trial iterate
to the trial iterate 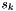 . The actual reduction is defined by
. The actual reduction is defined by
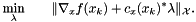
and the predicted reduction is given by
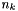
where
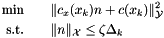
The following decision procedure is then used (we leave out the details of the penalty parameter update):
![\begin{enumerate} \addtocounter{enumi}{-1} \item Assume $0 < \eta_1 < \eta_2 < 1$, $0 < \gamma_1 < \gamma_2 < 1$. \item Acceptance Test. \begin{enumerate} \item Update penalty parameter $\rho_k$ (details omitted). \item Compute actual reduction $ared(s_k^x; \rho_k)$ and predicted reduction $pred(s_k^x; \rho_k)$, and their ratio $\theta_k=\frac{ared(s_k^x; \rho_k)}{pred(s_k^x; \rho_k)}$. \item If $\theta_k \ge \eta_1$, set $x_{k+1} = x_k+s_k$, otherwise set $x_{k+1} = x_k$ and reset $\lambda_{k+1} = \lambda_k$. \end{enumerate} \item Trust-Region Radius Update. Set \[ \Delta_{k+1} \in \begin{cases} [ \Delta_k, \infty] & \mbox{ if } \; \theta_k \ge \eta_2, \\ [ \gamma_2 \Delta_k, \Delta_k ] & \mbox{ if } \; \theta_k \in [\eta_1, \eta_2), \\ [ \gamma_1 \Delta_k, \gamma_2 \Delta_k ] & \mbox{ if } \; \theta_k < \eta_1. \end{cases} \] \end{enumerate}](form_46.png)
References Aristos::Vector::createVector(), Aristos::Vector::innerProd(), Aristos::Vector::linComb(), and runMultiplierEst().
Referenced by run().
| bool Aristos::SQPAlgo::runDerivativeCheck | ( | const Vector & | x, |
| const Vector & | l, | ||
| const Vector & | dir | ||
| ) |
Derivative checks..
| x | [in] - Iterate vector. |
| l | [in] - Lagrange multiplier vector. |
| dir | [in] - Direction of differentiation. |
true if runDerivativeCheck terminates successfully.Checks validity of the computation of the following quantities:
It is best to run the checks once before the SQP run, with random input vectors.
References Aristos::Vector::createVector().
| bool Aristos::SQPAlgo::runMultiplierEst | ( | const Vector & | x, |
| const Vector & | g, | ||
| Vector & | l, | ||
| double | tol | ||
| ) |
Computes a Lagrange multiplier estimate.
| x | [in] - Current SQP iterate. |
| g | [in] - Gradient of the objective. |
| l | [out] - The vector of Lagrange multipliers. |
| tol | [in] - Tolerance for inexact computations. |
true if runMultiplierEst is successful.Calls a user-defined multiplier estimate function which is passed in through the data pool object. We might provide a default routine in the future.
A common practice in SQP methods is to approximate the Lagrange multipliers by a least-squares estimate based on the KKT stationarity conditions (eq:eqstationarity}). Thus at each iterate $x_k$, we solve a problem related to the least-squares problem
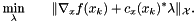
INEXACT VERSION:
It should be noted that there are many ways in which Lagrange multiplier estimation problems can be formulated, due to specific problem features and data representations provided by the user. The convergence theory for SQP methods poses rather loose requirements on the Lagrange multipliers. In fact, our SQP algorithm merely requires that the sequence of Lagrange multipliers be uniformly bounded.
This is guaranteed through our choice of the stopping criteria for the iterative linear system solver that computes the Lagrange multipliers.
Referenced by run(), runAcceptStep(), and runAcceptStepInx().
| bool Aristos::SQPAlgo::runQuasiNormalStep | ( | const Vector & | x, |
| const Vector & | c, | ||
| Vector & | s, | ||
| double | delta, | ||
| double | tol | ||
| ) |
Computes the quasi-normal step.
| x | [in] - Current SQP iterate. |
| c | [in] - The vector of constraint values. |
| s | [out] - The computed quasi-normal step vector. |
| delta | [in] - Scaled trust-region radius. |
| tol | [in] - Tolerance for inexact computations. |
true if runQuasiNormalStep is successful.We ask that the quasi-normal step 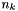 approximately solve a problem of the following type:
approximately solve a problem of the following type:
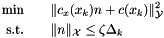
The approximate solution is computed using the Powell dogleg method. The dogleg path is computed using the Cauchy point 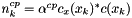 , where the step length
, where the step length 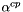 is given by
is given by
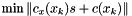
and the feasibility step 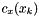 given, for example, as the minimum norm minimizer of the 2-norm of the linearized constraints (other choices are possible):
given, for example, as the minimum norm minimizer of the 2-norm of the linearized constraints (other choices are possible):
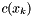
The intersection of the dogleg path (origin - Cauchy point - feasibility point) with the trust-region constraint gives the quasi-normal step.
INEXACT VERSION:
We require from the quasi-normal step 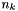 to give as much decrease as
to give as much decrease as 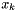 , and
, and
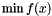
for some 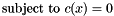 independent of
independent of 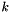 . Additionally, due to possible nonnormality of
. Additionally, due to possible nonnormality of 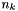 with respect to the tangent space of the constraints, the following condition must hold for
with respect to the tangent space of the constraints, the following condition must hold for 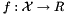 independent of
independent of 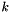 :
:
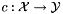
All of the above is guaranteed through our choice of the stopping criteria for an iterative linear system solver that computes the feasibility step 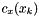 .
.
References Aristos::Vector::createVector(), Aristos::Vector::innerProd(), Aristos::Vector::linComb(), and Aristos::Vector::Set().
Referenced by run().
| bool Aristos::SQPAlgo::runTangentialStep | ( | const Vector & | x, |
| const Vector & | g, | ||
| const Vector & | v, | ||
| const Vector & | l, | ||
| Vector & | s, | ||
| double | delta, | ||
| int | cgitmax, | ||
| double | cgtol, | ||
| double | tol, | ||
| int & | cgiter, | ||
| int & | iflag | ||
| ) |
Computes the tangential step.
| x | [in] - Current SQP iterate. |
| g | [in] - Current gradient of the objective vector. |
| v | [in] - Current quasi-normal step. |
| l | [in] - Current Lagrange multiplier estimate. |
| s | [out] - The computed tangential step vector. |
| delta | [in] - Trust-region radius. |
| cgitmax | [in] - Maximum number of conjugate gradient iterations (internal use only). |
| cgtol | [in] - Stopping tolerance for the conjugate gradient method (internal use only). |
| tol | [in] - Tolerance for inexact computations. |
| cgiter | [out] - Required number of conjugate gradient iterations. |
| iflag | [out] - Return flag: 0 - normal convergence 1 - negative curvature detected 2 - trust-region radius active 3 - maximum number of conjugate gradient iterations exceeded |
true upon successful termination (not the same as convergence!) of runTangentialStep.The standard requirements on the tangential step are that it lie in the tangent space of the constraints and that it move the quadratic model of the Lagrangian toward optimality. Thus we ask that the tangential step 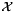 approximately solve a problem of the type
approximately solve a problem of the type

It is solved using the Steihaug variant of the conjugate gradient (CG) method. We use a projected CG method in the full space, rather than explicitly computing the null space of 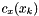 . This method relies on applications of the orthogonal projection operator
. This method relies on applications of the orthogonal projection operator 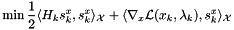 , defined by
, defined by
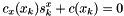
where 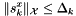 is the identity operator.
is the identity operator.
INEXACT VERSION:
As in the case of the quasi-normal step computation, the tangential step only needs to satisfy a fraction of the Cauchy decrease condition. The model function is in this case related to a quadratic model of the Lagrangian functional (we leave out the details).
Convergence in presence of inexactness is guaranteed through our choice of the stopping criteria for an iterative linear system solver that applies the projection operator 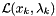 .
.
References Aristos::Vector::createVector(), Aristos::Vector::innerProd(), Aristos::Vector::linComb(), and Aristos::Vector::Set().
| bool Aristos::SQPAlgo::runTangentialStepInx | ( | const Vector & | x, |
| const Vector & | g, | ||
| const Vector & | v, | ||
| const Vector & | l, | ||
| Vector & | s, | ||
| double | delta, | ||
| int | cgitmax, | ||
| double | cgtol, | ||
| double | fixedtol, | ||
| bool | istolfixed, | ||
| bool | fullortho, | ||
| bool | orthocheck, | ||
| bool | fcdcheck, | ||
| int & | cgiter, | ||
| int & | iflag | ||
| ) |
Computes the tangential step using the inexact CG algorithm with full orthogonalization and inexactness control.
| x | [in] - Current SQP iterate. |
| g | [in] - Current gradient of the objective vector. |
| v | [in] - Current quasi-normal step. |
| l | [in] - Current Lagrange multiplier estimate. |
| s | [out] - The computed tangential step vector. |
| delta | [in] - Trust-region radius. |
| cgitmax | [in] - Maximum number of conjugate gradient iterations (internal use only). |
| cgtol | [in] - Stopping tolerance for the conjugate gradient method (internal use only). |
| fixedtol | [in] - Tolerance for inexact computations. |
| istolfixed | [in] - true, if fixed inexact solver tolerances are desired false, if the SQP algorithm is managing inexactness |
| fullortho | [in] - true, if full orthogonalization of search directions is desired false, if standard CG 2-vector orthogonalization is sufficient |
| orthocheck | [in] - true, if orthoganality of projected residuals is to be verified false, otherwise |
| fcdcheck | [in] - true, if the fraction of Cauchy decrease condition is to be verified false, otherwise |
| cgiter | [out] - Returns the required number of conjugate gradient iterations. |
| iflag | [out] - Return flag: 0 - normal convergence 1 - negative curvature detected 2 - trust-region radius active 3 - maximum number of conjugate gradient iterations exceeded |
true upon successful termination (not the same as convergence!) of runTangentialStep.The standard requirements on the tangential step are that it lie in the tangent space of the constraints and that it move the quadratic model of the Lagrangian toward optimality. Thus we ask that the tangential step 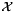 approximately solve a problem of the type
approximately solve a problem of the type

It is solved using the Steihaug variant of the conjugate gradient (CG) method. We use a projected CG method in the full space, rather than explicitly computing the null space of 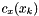 . This method relies on applications of the orthogonal projection operator
. This method relies on applications of the orthogonal projection operator 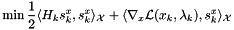 , defined by
, defined by
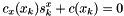
where 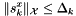 is the identity operator.
is the identity operator.
The tangential step only needs to satisfy a fraction of the Cauchy decrease condition. The model function is in this case related to a quadratic model of the Lagrangian functional (we leave out the details).
Convergence in presence of inexactness is guaranteed through our choice of the stopping criteria for an iterative linear system solver that applies the projection operator 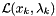 .
.
References Aristos::Vector::createVector(), Aristos::Vector::innerProd(), Aristos::Vector::linComb(), and Aristos::Vector::Set().
Referenced by run().
 1.8.6
1.8.6