Compute smallest eigenvalues of a generalized eigenvalue problem, using block Krylov-Schur with Epetra and an Amesos direct solver.This example computes the eigenvalues of smallest magnitude of a generalized eigenvalue problem 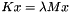 , using Anasazi's implementation of the block Krylov-Schur method, with Epetra linear algebra and a direct solver from the Amesos package.
, using Anasazi's implementation of the block Krylov-Schur method, with Epetra linear algebra and a direct solver from the Amesos package.
In the example, the "operator A such that \f$A z = K^{-1} M z\f$" is a subclass of Epetra_Operator. The Apply method of that operator takes the vector b, and computes 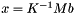 . It does so first by applying the matrix M, and then by solving the linear system
. It does so first by applying the matrix M, and then by solving the linear system 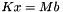 for x. Trilinos implements many different ways to solve linear systems. The example uses the sparse direct solver KLU to do so. Trilinos' Amesos package has an interface to KLU.
for x. Trilinos implements many different ways to solve linear systems. The example uses the sparse direct solver KLU to do so. Trilinos' Amesos package has an interface to KLU.
#include "Epetra_Map.h"
#include "Epetra_CrsMatrix.h"
#include "Epetra_LinearProblem.h"
#include "Amesos.h"
#include "ModeLaplace2DQ2.h"
#ifdef EPETRA_MPI
# include "Epetra_MpiComm.h"
#else
# include "Epetra_SerialComm.h"
#endif
public:
const bool useTranspose = false );
virtual ~AmesosGenOp () {}
const char*
Label()
const {
return "Operator that applies K^{-1} M or M K^{-T}";
}
return solver_->Comm ();
}
return massMtx_->OperatorDomainMap ();
}
return massMtx_->OperatorRangeMap ();
}
return -1;
};
double NormInf ()
const {
return -1.0; }
private:
AmesosGenOp () {};
AmesosGenOp (const AmesosGenOp& genOp);
bool useTranspose_;
};
int
main (int argc, char *argv[])
{
using std::cerr;
using std::cout;
using std::endl;
#ifdef EPETRA_MPI
MPI_Init (&argc, &argv);
#else
#endif // EPETRA_MPI
const int MyPID = Comm.
MyPID ();
const int space_dim = 2;
std::vector<double> brick_dim (space_dim);
brick_dim[0] = 1.0;
brick_dim[1] = 1.0;
std::vector<int> elements (space_dim);
elements[0] = 10;
elements[1] = 10;
RCP<ModalProblem> testCase =
rcp (
new ModeLaplace2DQ2 (Comm, brick_dim[0], elements[0],
brick_dim[1], elements[1]));
RCP<Epetra_CrsMatrix> K =
rcp (const_cast<Epetra_CrsMatrix* > (testCase->getStiffness ()),
false);
RCP<Epetra_CrsMatrix> M =
rcp (const_cast<Epetra_CrsMatrix* > (testCase->getMass ()),
false);
Amesos amesosFactory;
RCP<Amesos_BaseSolver> AmesosSolver;
const int numSolverNames = 9;
const char* solverNames[9] = {
"Klu", "Umfpack", "Superlu", "Superludist", "Mumps",
"Paradiso", "Taucs", "CSparse", "Lapack"
};
for (int k = 0; k < numSolverNames; ++k) {
const char* const solverName = solverNames[k];
if (amesosFactory.Query (solverName)) {
AmesosSolver =
rcp (amesosFactory.Create (solverName, AmesosProblem));
if (MyPID == 0) {
cout << "Amesos solver: \"" << solverName << "\"" << endl;
}
}
}
if (AmesosSolver.is_null ()) {
throw std::runtime_error ("Amesos appears not to have any solvers enabled.");
}
AmesosSolver->SymbolicFactorization ();
AmesosSolver->NumericFactorization ();
double tol = 1.0e-8;
int nev = 10;
int blockSize = 3;
int numBlocks = 3 * nev / blockSize;
int maxRestarts = 5;
std::string which = "LM";
MyPL.
set (
"Verbosity", verbosity);
MyPL.
set (
"Which", which);
MyPL.
set (
"Block Size", blockSize);
MyPL.
set (
"Num Blocks", numBlocks);
MyPL.
set (
"Maximum Restarts", maxRestarts);
MyPL.
set (
"Convergence Tolerance", tol);
RCP<MV> ivec =
rcp (
new MV (K->Map (), blockSize));
ivec->Random ();
RCP<AmesosGenOp> Aop =
rcp (
new AmesosGenOp (AmesosSolver, M));
RCP<Anasazi::BasicEigenproblem<double,MV,OP> > MyProblem =
MyProblem->setHermitian (true);
MyProblem->setNEV (nev);
const bool boolret = MyProblem->setProblem ();
if (boolret != true) {
if (MyPID == 0) {
cerr << "Anasazi::BasicEigenproblem::setProblem() returned with error." << endl;
}
#ifdef EPETRA_MPI
MPI_Finalize ();
#endif // EPETRA_MPI
return -1;
}
cout << "Anasazi eigensolver did not converge." << endl;
}
std::vector<Anasazi::Value<double> > evals = sol.
Evals;
RCP<MV> evecs = sol.
Evecs;
if (numev > 0) {
MV tempvec (K->Map (), MVT::GetNumberVecs (*evecs));
K->Apply (*evecs, tempvec);
MVT::MvTransMv (1.0, tempvec, *evecs, dmatr);
if (MyPID == 0) {
double compeval = 0.0;
cout.setf (std::ios_base::right, std::ios_base::adjustfield);
cout << "Actual Eigenvalues (obtained by Rayleigh quotient) : " << endl;
cout << "------------------------------------------------------" << endl;
cout << std::setw(16) << "Real Part"
<< std::setw(16) << "Rayleigh Error" << endl;
cout << "------------------------------------------------------" << endl;
for (int i = 0; i < numev; ++i) {
compeval = dmatr(i,i);
cout << std::setw(16) << compeval
<< std::setw(16)
<< std::fabs (compeval - 1.0/evals[i].realpart)
<< endl;
}
cout << "------------------------------------------------------" << endl;
}
}
#ifdef EPETRA_MPI
MPI_Finalize ();
#endif // EPETRA_MPI
return 0;
}
AmesosGenOp::
const bool useTranspose)
: solver_ (solver),
massMtx_ (massMtx),
problem_ (NULL),
useTranspose_ (useTranspose)
{
throw std::invalid_argument ("AmesosGenOp constructor: The 'solver' "
"input argument is null.");
}
throw std::invalid_argument ("AmesosGenOp constructor: The 'massMtx' "
"input argument is null.");
}
if (problem == NULL) {
throw std::invalid_argument ("The solver's GetProblem() method returned "
"NULL. This probably means that its "
"LinearProblem has not yet been set.");
}
problem_ = problem;
if (solver_->UseTranspose ()) {
solver_->SetUseTranspose (! useTranspose);
} else {
solver_->SetUseTranspose (useTranspose);
}
if (massMtx_->UseTranspose ()) {
massMtx_->SetUseTranspose (! useTranspose);
} else {
massMtx_->SetUseTranspose (useTranspose);
}
}
int
AmesosGenOp::SetUseTranspose (bool useTranspose)
{
int err = 0;
if (problem_ == NULL) {
throw std::logic_error ("AmesosGenOp::SetUseTranspose: problem_ is NULL");
}
if (massMtx_.is_null ()) {
throw std::logic_error ("AmesosGenOp::SetUseTranspose: massMtx_ is null");
}
if (solver_.is_null ()) {
throw std::logic_error ("AmesosGenOp::SetUseTranspose: solver_ is null");
}
const bool solverUsesTranspose = solver_->UseTranspose ();
if (solverUsesTranspose) {
err = solver_->SetUseTranspose (! useTranspose);
} else {
err = solver_->SetUseTranspose (useTranspose);
}
if (err != 0) {
return err;
}
if (massMtx_->UseTranspose ()) {
err = massMtx_->SetUseTranspose (! useTranspose);
} else {
err = massMtx_->SetUseTranspose (useTranspose);
}
if (err != 0) {
(void) solver_->SetUseTranspose (solverUsesTranspose);
return err;
}
useTranspose_ = useTranspose;
return 0;
}
int
{
if (problem_ == NULL) {
throw std::logic_error ("AmesosGenOp::Apply: problem_ is NULL");
}
if (massMtx_.is_null ()) {
throw std::logic_error ("AmesosGenOp::Apply: massMtx_ is null");
}
if (solver_.is_null ()) {
throw std::logic_error ("AmesosGenOp::Apply: solver_ is null");
}
if (! useTranspose_) {
massMtx_->Apply (X, MX);
Y.PutScalar (0.0);
problem_->SetRHS (&MX);
problem_->SetLHS (&Y);
solver_->Solve ();
}
else {
problem_->SetRHS (&tmpX);
problem_->SetLHS (&ATX);
solver_->Solve ();
massMtx_->Apply (ATX, Y);
}
return 0;
}
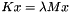 , using Anasazi's implementation of the block Krylov-Schur method, with Epetra linear algebra and a direct solver from the Amesos package.
, using Anasazi's implementation of the block Krylov-Schur method, with Epetra linear algebra and a direct solver from the Amesos package.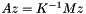 .
.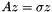 , which is a spectral transformation of the original problem
, which is a spectral transformation of the original problem 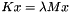 .
.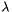 of the original problem are the inverses of the eigenvalues
of the original problem are the inverses of the eigenvalues 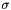 of the transformed problem.
of the transformed problem.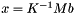 . It does so first by applying the matrix M, and then by solving the linear system
. It does so first by applying the matrix M, and then by solving the linear system 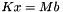 for x. Trilinos implements many different ways to solve linear systems. The example uses the sparse direct solver KLU to do so. Trilinos' Amesos package has an interface to KLU.
for x. Trilinos implements many different ways to solve linear systems. The example uses the sparse direct solver KLU to do so. Trilinos' Amesos package has an interface to KLU. 1.8.5
1.8.5