|
Galeri
Development
|
This file first gives an example of how to create an Epetra_CrsMatrix object, then it details the supported matrices and gives a list of required parameters.
Given an already created Epetra_Map, Galeri can construct an Epetra_CrsMatrix object that has this Map as RowMatrixRowMap(). A simple example is as follows. Let Map be an already created Epetra_Map* object; then, a diagonal matrix with 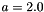 on the diagonal can be created using the instructions
on the diagonal can be created using the instructions
#include "Galeri_CrsMatrices.h"
using namespace Galeri;
...
string MatrixType = "Diag";
List.set("a", 2.0);
Epetra_CrsMatrix* Matrix = CreateCrsMatrix(MatrixType, Map, List);
More interesting matrices can be easily created. For example, a 2D biharmonic operator can be created like this:
List.set("nx", 10);
List.set("ny", 10);
Epetra_CrsMatrix* Matrix = Galeri.Create("Biharmonic2D", Map, List);
For matrices arising from 2D discretizations on Cartesian grids, it is possible to visualize the computational stencil at a given grid point by using function PrintStencil2D, defined in the Galeri namespace:
#include "Galeri_Utils.h" using namespace Galeri; ... // Matrix is an already created Epetra_CrsMatrix* object // and nx and ny the number of nodes along the X-axis and Y-axis, // respectively. PrintStencil2D(Matrix, nx, ny);
The output is:
2D computational stencil at GID 12 (grid is 5 x 5)
0 0 1 0 0
0 2 -8 2 0
1 -8 20 -8 1
0 2 -8 2 0
0 0 1 0 0
To present the list of supported matrices we adopt the following symbols:
Cartesian2D. The values of nx and ny are still available in the input list;Cartesian3D. The values of nx, ny and nz are still available in the input list;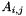 indicates the
indicates the 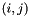 matrix of the element in MATLAB notation (that is, starting from 1).
matrix of the element in MATLAB notation (that is, starting from 1).The list of supported matrices is now reported in alphabetical order.
BentPipe2D (MAP2D, PAR): Returns a matrix corresponding to the finite-difference discretization of the problem
![\[ - \epsilon \Delta u + (v_x,v_y) \cdot \nabla u = f \]](form_4.png)
![\[ v_x = 2 conv x (x/2 - 1) (1 - 2y), \quad \quad \quad v_y =-4 conv y (y - 1) (1 - x) \]](form_5.png)
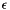 can be specified using
can be specified using diff, and that of 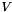 using
using conv. The default values are diff=1e-5, conv=1.BigCross2D (MAP2D, PAR): Creates a matrix corresponding to the following stencil:
![\[ \left[ \begin{tabular}{ccccc} & & ee & & \\ & & e & & \\ bb & b & a & c & cc \\ & & d & & \\ & & dd & & \\ \end{tabular} \right] . \]](form_8.png)
Laplace2DFourthOrder. A non-default value must be set in the input parameter list before creating the matrix. For example, to specify the value of 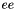 , one should do
, one should do List.set("ee", 12.0);
Matrix = Galeri.Create("BigCross2D", Map, List);BigStar2D (MAP2D, PAR): Creates a matrix corresponding to the stencil
![\[ \left[ \begin{tabular}{ccccc} & & ee & & \\ & z3 & e & z4 & \\ bb & b & a & c & cc \\ & z1 & d & z2 & \\ & & dd & & \\ \end{tabular} \right] . \]](form_10.png)
Biharmonic2D.Biharmonic2D (MAP2D, PAR): Creates a matrix corresponding to the discrete biharmonic operator,
![\[ \frac{1}{h^4} \; \left[ \begin{tabular}{ccccc} & & 1 & & \\ & 2 & -8 & 2 & \\ 1 & -8 & 20 & -8 & 1 \\ & 2 & -8 & 2 & \\ & & 1 & & \\ \end{tabular} \right] . \]](form_11.png)
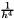 scaling.
scaling.Cauchy (MAP, MATLAB, DENSE, PAR): Creates a particular instance of a Cauchy matrix with elements 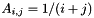 . Explicit formulas are known for the inverse and determinant of a Cauchy matrix. For this particular Cauchy matrix, the determinant is nonzero and the matrix is totally positive.
. Explicit formulas are known for the inverse and determinant of a Cauchy matrix. For this particular Cauchy matrix, the determinant is nonzero and the matrix is totally positive.Cross2D (MAP2D, PAR): Creates a matrix with the same stencil of Laplace2D}, but with arbitrary values. The computational stencil is
![\[ \left[ \begin{tabular}{ccc} & e & \\ b & a & c \\ & d & \\ \end{tabular} \right] . \]](form_14.png)
The default values are
List.set("a", 4.0);
List.set("b", -1.0);
List.set("c", -1.0);
List.set("d", -1.0);
List.set("e", -1.0);For example, to approximate the 2D Helmhotlz equation
![\[ - \nabla u - \sigma u = f \quad \quad (\sigma \geq 0) \]](form_15.png)
with the standard 5-pt discretization stencil
![\[ \frac{1}{h^2} \; \left[ \begin{tabular}{ccc} & -1 & \\ -1 & $4 -\sigma h^2$ & -1 \\ & -1 & \\ \end{tabular} \right] \]](form_16.png)
and 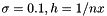 , one can set
, one can set
List.set("a", 4 - 0.1 * h * h);
List.set("b", -1.0);
List.set("c", -1.0);
List.set("d", -1.0);
List.set("e", -1.0); The factor 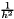 can be considered by scaling the input parameters.
can be considered by scaling the input parameters.
Cross3D (MAP3D, PAR): Similar to the Cross2D case. The matrix stencil correspond to that of a 3D Laplace operator on a structured 3D grid. On a given x-y plane, the stencil is as in Laplace2D. The value on the plane below is set using f, the value on the plane above with g.Diag (MAP, PAR): Creates 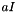 , where
, where 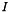 is the identity matrix of size
is the identity matrix of size n. The default value is List.set("a", 1.0);Fiedler (MAP, MATLAB, DENSE, PAR): Creates a matrix whose element are 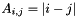 . The matrix is symmetric, and has a dominant positive eigenvalue, and all the other eigenvalues are negative.
. The matrix is symmetric, and has a dominant positive eigenvalue, and all the other eigenvalues are negative.Hanowa (MAP, MATLAB, PAR): Creates a matrix whose eigenvalues lie on a vertical line in the complex plane. The matrix has the 2x2 block structure (in MATLAB's notation)
![\[ A = \left[ \begin{tabular}{cc} a * eye(n/2) & -diag(1:m) \\ diag(1:m) & a * eye(n/2) \\ \end{tabular} \right]. \]](form_22.png)
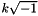 and
and 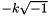 , for
, for 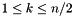 . The default value is
. The default value is List.set("a", -1.0);
Hilbert (MAP, MATLAB, DENSE, PAR): This is a famous example of a badly conditioned matrix. The elements are defined in MATLAB notation as 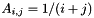 .
.JordanBlock (MAP, MATLAB, PAR): Creates a Jordan block with eigenvalue lambda. The default value is lambda=0.1;KMS (MAP, MATLAB, DENSE, PAR): Create the 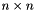 Kac-Murdock-Szego Toepliz matrix such that
Kac-Murdock-Szego Toepliz matrix such that 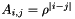 (for real
(for real 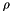 only). Default value is
only). Default value is 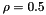 , or can be using
, or can be using rho. The inverse of this matrix is tridiagonal, and the matrix is positive definite if and only if 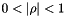 . The default value is
. The default value is rho=-0.5;Laplace1D (MAP, PAR): Creates the classical tridiagonal matrix with stencil ![$ [-1, 2, -1] $](form_31.png) .
.Laplace1DNeumann (MAP, PAR): As for Laplace1D, but with Neumann boundary conditioners. The matrix is singular.Laplace2D (MAP2D, PAR): Creates a matrix corresponding to the stencil of a 2D Laplacian operator on a structured Cartesian grid. The matrix stencil is:
![\[ \frac{1}{h^2} \; \left[ \begin{tabular}{ccc} & -1 & \\ -1 & 4 & -1 \\ & -1 & \\ \end{tabular} \right] . \]](form_32.png)
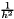 scaling.
scaling.Laplace2DFourthOrder (MAP2D, PAR): Creates a matrix corresponding to the stencil of a 2D Laplacian operator on a structured Cartesian grid. The matrix stencil is:
![\[ \frac{1}{12 h^2} \; \left[ \begin{tabular}{ccccc} & & 1 & & \\ & & -16 & & \\ 1 & -16 & 60 & -16 & 1 \\ & & -16 & & \\ & & 1 & & \\ \end{tabular} \right] . \]](form_33.png)
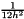 scaling.
scaling.Laplace3D (MAP3D, PAR): Creates a matrix corresponding to the stencil of a 3D Laplacian operator on a structured Cartesian grid.Lehmer (MAP, MATLAB, DENSE, PAR): Returns a symmetric positive definite matrix, such that
![\[ A_{i,j} = \left\{ \begin{array}{ll} \frac{i}{j} & \mbox{ if } j \ge i \\ \frac{j}{i} & \mbox{ otherwise } \\ \end{array} \right. . \]](form_35.png)
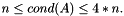
Minij (MAP, MATLAB, DENSE, PAR): Returns the symmetric positive definite matrix defined as 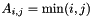 .
.Ones (MAP, PAR): Returns a matrix with 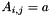 . The default value is
. The default value is a=1;Parter (MAP, MATLAB, DENSE, PAR): Creates a matrix 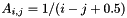 . This matrix is a Cauchy and a Toepliz matrix. Most of the singular values of A are very close to
. This matrix is a Cauchy and a Toepliz matrix. Most of the singular values of A are very close to 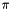 .
.Pei (MAP, MATLAB, DENSE, PAR): Creates the matrix
![\[ A_{i,j} = \left\{ \begin{array}{cc} \alpha + 1 & \mbox{ if } i \neq j \\ 1 & \mbox{ if } i = j. \end{array} \right. . \]](form_41.png)
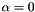 or
or 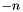 . The default value for
. The default value for 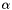 is 1.0.
is 1.0.Recirc2D (MAP2D, PAR): Returns a matrix corresponding to the finite-difference discretization of the problem
![\[ - \epsilon \Delta u + (v_x,v_y) \cdot \nabla u = f \]](form_4.png)
![\[ v_x = conv \cdot 4 x (x - 1) (1 - 2y), \quad \quad \quad v_y = -conv \cdot 4 y (y - 1) (1 - 2x) \]](form_45.png)
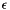 can be specified using
can be specified using diff, and that of 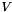 using
using conv. The default values are diff=1e-5, conv=1.Ris (MAP, MATLAB, PAR): Returns a symmetric Hankel matrix with elements 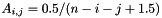 , where
, where 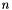 is problem size. The eigenvalues of A cluster around
is problem size. The eigenvalues of A cluster around 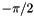 and
and 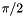 .
.Star2D (MAP2D, PAR): Creates a matrix with the 9-point stencil:
![\[ \left[ \begin{tabular}{ccc} z3 & e & z4 \\ b & a & c \\ z1 & d & z2 \\ \end{tabular} \right] . \]](form_50.png)
List.set("a", 8.0);
List.set("b", -1.0);
List.set("c", -1.0);
List.set("d", -1.0);
List.set("e", -1.0);
List.set("z1", -1.0);
List.set("z2", -1.0);
List.set("z3", -1.0);
List.set("z4", -1.0);Stretched2D (MAP2D, PAR): Creates a matrix corresponding to the following stencil:
![\[ \left[ \begin{tabular}{ccc} -1.0 & $-4.0 + \epsilon$ & -1.0 \\ $2.0 - \epsilon$ & 8.0 & $2.0 - \epsilon$ \\ -1.0 & $-4.0 + \epsilon$ & -1.0 \\ \end{tabular} \right] . \]](form_51.png)
epsilon=0.1;Tridiag (MAP, PAR): Creates a tridiagonal matrix with stencil
![\[ \left[ \begin{tabular}{ccc} b & a & c \\ \end{tabular} \right] . \]](form_52.png)
List.set("a", 2.0);
List.set("b", -1.0);
List.set("c", -1.0);UniFlow2D (MAP2D, PAR): Returns a matrix corresponding to the finite-difference discretization of the problem
![\[ - \epsilon \Delta u + (v_x,v_y) \cdot \nabla u = f \]](form_4.png)
![\[ v_x = cos(\alpha) V, \quad \quad \quad v_y = sin(\alpha) V \]](form_53.png)
List.set("alpha", .0);
List.set("diff", 1e-5);
List.set("conv", 1.0);  1.8.5
1.8.5