|
Epetra
Development
|
A lesson on parallel distributions and distributed objects.
In this lesson, we will explain how to create the simplest kind of Epetra linear algebra object: an Epetra_Vector, whose entries are distributed over the process(es) in a communicator. The Epetra_Map object describes this distribution of entries over processes. You create a Map to describe the distribution scheme you want, and then use the Map to create objects (such as Vectors) that have this distribution. We spend a little bit more time than you might initially wish explaining Map, but understanding it is important for getting the best performance out of Epetra. We give examples of different distributions you can create, use their Maps to create Vectors, and then do some arithmetic with the Vectors.
Epetra uses objects called "Maps" to encapsulate the details of distributing data over MPI processes. Maps make data distribution into a first-class citizen. Each Map instance represents a particular data distribution.
You can think of a Map instance abstractly as representing a vector space. If two vectors have the same map, it's like they come from the same vector space. For example, you can add them together without performing communication. If they come from different vector spaces, then you need more information to know whether it is legal to add the vectors together.
You can find documentation for Epetra's Map class here.
For you as the user, the fact that you might be parallelizing your application using MPI is really an implementation detail. You care about what we call global indices. These represent the entries of a distributed object (such as rows or columns of a sparse matrix, or entries of a vector) uniquely over the entire object. The object in turn may be distributed over multiple processes. Just about any data structure containing entries that can be assigned an integer index can be distributed using a Map. For most Epetra users, this means entries of a vector, rows of an Epetra_MultiVector, or rows or columns of a sparse graph or matrix. However, it is not limited to these kinds of objects. You may even use Map for your own distributed objects.
A Map assigns global indices to parallel processes. If it assigns a global index G to a process P, we say that process P owns global index G. It is legal for multiple processes to own the same global index G. In fact, this is how we implement many useful communication patterns, including those in sparse matrix-vector multiply. We won't go into much detail in this lesson about that.
For efficiency, within a process, we refer to a global index using its "local index" on that process. Local indices are local to the process that owns them. If process P owns global index G, then there is a unique local index L on process P corresponding to G. If the local index L is valid on process P, then there is a unique global index G owned by P corresponding to the pair (L, P). However, multiple processes might own the same global index, so a global index G might correspond to multiple (L, P) pairs. In summary, local indices on a process correspond to object "entries" (e.g., sparse matrix rows or columns) owned by that process.
Local indices matter to you because it may be more efficient to use them to access or modify local data than it is to use global indices. This is because distributed data structures must convert from global to local indices every time a user asks for an element by its global index. This requires a table lookup in general, since a process may own an arbitrary subset of all the global indices, in an arbitrary order. Even though local indices are an implementation detail, we expose them because avoiding that table lookup on each access can improve performance a lot.
If a Map has N global entries over P processes, and if no one process owns all the global entries, we never store all N global indices on a single process. Some kinds of Maps require storing all the global indices, but in this case, the indices are themselves distributed over processes. This ensures memory scalability (no one process has to store all the data).
We mentioned above that a Map behaves much like a vector space. For instance, if two Vectors have the same Map, it is both legal and meaningful to add them together. This makes it useful to be able to compare Maps. There are two ways to compare two Maps. Two Maps map1 and map2 may either be "compatible" or "the
same" (map1.SameAs(map2)).
Compatibility of two Maps corresponds to isomorphism of two vector spaces. Two Maps that are the same are always compatible. The compatibility criterion is less restrictive than the "sameness" criterion. Adding together two vectors with compatible but not the same Maps is legal. It might not make mathematical sense, depending on your application. This is because entries of the vectors are ordered differently. (Also, just because two vector spaces are isomorphic, doesn't necessarily mean that adding entries of one to entries of another makes sense.) Adding together two vectors with the same Maps is both legal and mathematically sensible.
Both sameness and compatibility are commutative Boolean relations: for example, map1.SameAs(map2) means map2.SameAs(map1).
Two Maps are compatible when:
Two Maps are the same when:
In Epetra, local indices have type int. On most systems today, this is a 32-bit unsigned integer. Originally, global ordinals could only have type int as well. This meant that one could only solve problems with 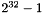 (about two billion) "things" (e.g., unknowns or matrix entries) in them. Many Epetra users now want to solve even larger problems. As a result, we added a configure-time option to build Epetra with 64-bit global indices, of type
(about two billion) "things" (e.g., unknowns or matrix entries) in them. Many Epetra users now want to solve even larger problems. As a result, we added a configure-time option to build Epetra with 64-bit global indices, of type long long. This option is disabled by default, since some C++ compilers do not implement the long long type. (It is part of the C++11 language standard, but some C++98 compilers provide it as an extension of their C99 support.) The long long type must be at least 64 bits long, and is signed.
A Map is one to one if each global index in the Map is owned by only one process. This means that the function from global index G to its local index and process rank (L,P) is one to one in a mathematical sense ("injective"). In this case, the function is only onto ("surjective") if there is only one process. Knowing whether a Map is one-to-one is important for data redistribution, which Epetra exposes as the Epetra_Import and Epetra_Export operations. We will cover Import and Export in subsequent lessons.
An example of a one-to-one Map is a Map containing 101 global indices 0 .. 100 and distributed over four processes, where
An example of a not one-to-one Map is a Map containing 101 global indices 0 .. 100 and distributed over four processes, where
Note the overlap of one global index between each "adjacent" process. An example of a mathematical problem with an overlapping distribution like this would be a 1-D linear finite element or finite difference discretization, where entries are distributed with unique ownership among the processes, but the boundary node between two adjacent entries on different processes is shared among those two processes.
A Map is contiguous when each process' list of global indices forms an interval and is strictly increasing, and the globally minimum global index equals the index base. Map optimizes for the contiguous case. In particular, noncontiguous Maps require communication in order to figure out which process owns a particular global index.
Note that in Epetra, "contiguous" is an optimization, not a predicate. Epetra may not necessarily work hard to check contiguity. The best way to ensure that your Map is contiguous is to use one of the two constructors that always make a contiguous Map.
An example of a contiguous Map is one containing 101 global indices 0 .. 100 and distributed over four processes, where
Note that Process 3 in this example owns 26 global indices, whereas the other processes each own 25. We say that a Map is uniform if each process owns the same number of global indices. The above Map is not uniform. Map includes both a constructor for uniform contiguous Maps, where you specify the total number of global indices, and a constructor for possibly nonuniform contiguous Maps, where you specify the number of global indices owned by each process.
Globally distributed means that all of the following are true:
If at least one of the above are not true, then we call the Map locally replicated. The two terms are mutually exclusive.
Epetra_Vector implements a finite-dimensional vector distributed over processes. Epetra_Vector inherits from the Epetra_MultiVector class, which represents a collection of one or more vectors with the same Map. Trilinos' solvers favor block algorithms, so they favors MultiVectors over single Vectors. A single Vector is just a MultiVector containing one vector, with a few convenience methods. You'll find documentation for Epetra's Vector class here.
Vector's interface contains some common linear algebra operations for vector-vector operations, including operations analogous to those in the BLAS 1 standard.
The following example follows the same initialization steps as in the previous lesson. It then creates two distributed Maps and some vectors, and does a few computations with the vectors.
The following example follows the same initialization steps as in the previous lesson. It then creates a distributed Epetra_Map and a Epetra_Vector, and shows how to read and modify the entries of the Epetra_Vector.
This lesson introduces one new topic: namely, the Teuchos memory management classes like Teuchos::Array. We will explain them here.
Teuchos::Array is an array container, templated on the type of objects that it contains. It behaves much like std::vector. The difference is that Array interoperates with the other Teuchos memory management classes. For example, Teuchos::ArrayView is a nonowning, nonpersistent view of part or all of an Array. The std::vector class does not have nonowning views; passing std::vector by value copies the data, and there is no way to get a view of part of the std::vector. Array and ArrayView fix these deficiencies. Teuchos::ArrayRCP is the array analog of !RCP; it allows shared ownership of an array. For more details, please refer to the reference guide to the Teuchos Memory Management Classes.
 1.8.5
1.8.5